Abstract: The Square of
Opposition is reviewed, and three additional inferences are explained and illustrated:
conversion, obversion, and contraposition.
I. The relations of the Traditional Square of Opposition may be conveniently defined as
follows. |
|
A. Contradictories (holds between the A and O;
and separately between the E and I): The statements cannot both be true and
cannot both be false. In other words, these respective statements have opposite truth
values. |
|
B. Contraries (hold between the A and E):
The statements cannot both be true, otherwise the truth value cannot be determined. |
|
C. Subcontraries (holds between the I and O):
The statements cannot both be false, otherwise the truth value cannot be determined. |
|
D. Subalternation (holds between the A and I;
and separately between the I and O): In reference to the Square, truth goes
down and falsity goes up, otherwise the resultant truth value cannot be determined. The
superaltern implies the subaltern. More precisely, |
|
|
If the superaltern is true, then the subaltern is true. |
|
|
If the superaltern is false, then the subaltern is undetermined. |
|
|
If the subaltern is true, then the superaltern is undetermined. |
|
|
If the subaltern is false, then the superaltern is false. |
| II. Mnemonic Device for remembering the Square of
Opposition. |
|
A. If you picture God at the top of the Square of Opposition
and the Devil at the bottom of the Square and remember the phrase "cannot both be
..." for contraries and subcontraries, the following mnemonic device might be
helpful. For clarity, refer to a copy of the Square of Opposition. |
|
B. The big "X" across the center of the Square
represents contradictories with opposite truth values--This should be very straightforward
to remember. |
|
C. Since "God" (or "truth") is at the
top of the diagram, contraries "cannot both be ... (you plug in) true." |
|
D. Since "the Devil"(or "falsity") is at
the bottom of the diagram, subcontraries "cannot both be ...(you plug in) false. |
|
E. With subalternation, "God" can send
"truth" down, but we wouldn't know what it would mean for "God" to
send "falsity" down (hence, this would be undetermined). But, "the
Devil" can send "falsity" up (since this is what Devils are good at), and
we would not know what it would mean for "the Devil" to send "truth"
up, so that would be undetermined in truth value. |
| III. "Bouncing Around the Square of Opposition." |
|
A. Suppose we know that a given O proposition of the
form "Some S is not P" is false. How many ways could we determine
the truth value of the corresponding I proposition ("Some S is P")? |
|
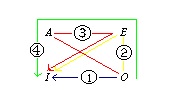
B. There are, of course, an indefinite number of ways
(assuming one can oscillate between two propositions). Consider the following four routes: |
 |
|
C. Notice that we could set an itinerary of our journey
along the selected four routes. The "reason," given below, is, so to speak, our
"inference ticket" for travel. |
|
|
Route
1: O to I |
|
|
|
Statement |
Reason |
Truth Value |
|
|
|
1. Some S is not P. |
given |
false |
|
|
|
2. Some S is P. |
subcontrariety |
true |
|
|
|
|
Route
2: O to E to I |
|
|
|
Statement |
Reason |
Truth Value |
|
|
|
1. Some S is not P. |
given |
false |
|
|
|
2. No S is P. |
subalternation |
false |
|
|
|
3. Some S is P. |
contradictory |
true |
|
|
|
|
Route
3: O to A to E to I |
|
|
|
Statement |
Reason |
Truth Value |
|
|
|
1. Some S is not P. |
given |
false |
|
|
|
2. All S is P. |
contradictory |
true |
|
|
|
3. No S is P. |
contrariety |
false |
|
|
|
4. Some S is P. |
contradictory |
true |
|
|
|
|
One would think that if our logic were consistent, all
possible routes from the false O to the I would result in a false truth
value for the I. But consider the following case--Route 4. |
|
|
|
|
Route
4: O to E to A to I |
|
|
|
Statement |
Reason |
Truth Value |
|
|
|
1. Some S is not P. |
given |
false |
|
|
|
2. No S is P. |
subalternation |
false |
|
|
|
3. All S is P. |
contrariety |
undetermined |
|
|
|
4. Some S is P. |
subalternation |
undetermined |
|
|
|
|
The final undetermined truth value for the I proposition
indicates part of the nature of immediate inferences. The logical relations involve
deduction but not reflection. Some premisses contain different "logical force"
than others. Examine for yourself how this is so. When you change quantity or quality,
there is a change in logical import. |
| III. Further Immediate Inferences: these logical
relations are not part of the Square of Opposition. They involve changes to the
subject and predicate classes. (The logical relations on the Square of Opposition always
keep the same subject and predicate terms) |
|
A. Conversion: interchanging the subject and
predicate terms of a categorical proposition (it is valid, or preserves the truth value)
for the E and I propositions only) |
|
|
1. Notice that the truth value is preserved for those
statements with symmetrical distribution status: the E and I. |
|
|
2. If an A or O proposition is converted, an
undetermined truth value results. |
|
|
3. The complete table for conversion is as
follows. Note especially that we are not reversing the subject and predicate positions.
Only the terms in the subject and predicate are interchanged. For this reason, it
might be helpful to invent actual classes for S and P when you first study
the relations. |
|
|
If "All S is P" is
given true, then "All P is S" is undetermined. |
|
|
If "All S is P" is
given false, then "All P is S" is undetermined. |
|
|
If "No S is P" is
given true, then "No P is S" is true. |
|
|
If "No S is P" is
given false, then "No P is S" is false. |
|
|
If "Some S is P"
is given true, then "Some P is S" is true. |
|
|
If "Some S is P"
is given false, then "Some P is S is false. |
|
|
If "Some S is not P"
is given true, then "Some P is not S" is undetermined. |
|
|
If "Some S is not P"
is given false, then "Some P is not S" is undetermined. |
|
|
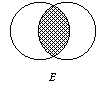
4. Another way to remember that only
the E and I statements preserve the truth value in conversion is to
note that flipping the E and I Venn Diagrams over results in the same
logical geography being displayed. I.e., their diagrams are symmetrical
respectively. |
 |
|
 |
|
B. Obversion: changing the quality and replacing the
predicate term with its complementary class (valid, or preserves truth value for all
propositions--the A, E, I, and O). |
|
|
1. The complementary class is the class of everything
not in the original class. E.g., the complementary class of "lightbulbs" is
"non-lightbulbs." Usually, one just tacks on "non-" to obtain a
complementary class. But note that the complementary class of "light bulbs" is
not "nonlight bulbs." |
|
|
2. Often, in English, certain prefixes indicate
complementary classes. For example, "un-," "in-," "de-,"
"im-," "dis-" and others are sometimes so used. However, English being
what it is, relying on the prefixes is risky. Consider "ravel" and
"unravel" or "flammable" and "inflammable" or
"imflammable." For this reason, it is usually safer to use the prefix
"non-" in a kind of logical pseudo-English. |
|
|
3. Often common sense requires thinking what the true
complement of a class is to be. The complementary class of "objects to be
admired" cannot be "non-objects to be admired." Sometimes, only the context
of the argument yields a clue as to the complementary class. Be careful not to empty your
classes--there are fundamental philosophical implications here. |
|
|
4. The complete table for obversion is as
follows. |
|
|
If "All S is P" is
given true, then "No S is non-P" is true. |
|
|
|
If "All S is P" is
given false, then "No S is non-P" is false. |
|
|
|
If "No S is P" is
given true, then "All S in non-P" is true. |
|
|
|
If "No S is P" is
given false, then "All S is non-P" is false. |
|
|
|
If "Some S is P" is
given true, then "Some S is not non-P" is true. |
|
|
|
If "Some S is P" is
given false, then "Some S is not non-P" is false. |
|
|
|
If "Some S is not P" is
given true, then "Some S is non-P" is true. |
|
|
|
If "Some S is not P" is
given false, then "Some S is non-P" is false. |
|
|
C. Contraposition: replacing the subject term by the
complement of its predicate term and replace the predicate term by the complement of its
subject term (valid, or preserves truth value only for the A and O propositions). |
|
|
1. Notice that contraposition is the same thing as
successive obversion, conversion, and obversion of a proposition. In effect,
contraposition does these operations in one step. Compare the following two inferences. |
|
|
Statement |
Reason |
Truth Value |
|
|
|
1. All S are P. |
given |
true |
|
|
|
2. All non-P is non-S. |
contraposition |
true |
|
|
|
Statement |
Reason |
Truth Value |
|
|
|
1. All S are P. |
given |
true |
|
|
|
2. No S are non-P. |
obversion |
true |
|
|
|
3. No non-P is S. |
conversion |
true |
|
|
|
4. All non-P is non-S. |
obversion |
true |
|
|
|
2. It might be helpful to visualize this picture of the general operation of
contraposition. |
|
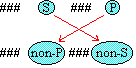 |
|
|
|
3. Again for contraposition, as for obversion, one has to be
careful about describing the class complement for exactness. |
|
|
4. The table for all the contrapositives is
as follows. |
|
|
If "All S is P" is
given true, then "All non-P is non-S" is true. |
|
|
If "All S is P" is
given false, then "All non-P is non-S" is false. |
|
|
If "No S is P" is given
true, then "No non-P is non-S" is undetermined. |
|
|
If "No S is P" is
given false, then "No non-P is non-S" is undetermined. |
|
|
If "Some S is P"
is given true, then "Some non-P is non-S" is undetermined. |
|
|
If "Some S is P"
is given false, then "Some non-P is non-S" is undetermined. |
|
|
If "Some S is not P"
is given true, then "Some non-P is not non-S" is true. |
|
|
If "Some S is not P"
is given false, then "Some non-P is not non-S" is false. |
| IV. To understand thoroughly these logical relations, work
problems, problems, and more problems. These logical relations are important in everyday
life as the use of ordinary language makes inferences even more difficult.
For practical
everyday examples, see these inference
examples. For
standard-form examples, practice with the quiz on Further
Immediate Inferences.
|
|
Note: Apply the general rules when making immediate
inferences. Memorizing tables is of little help for understanding the logical relations
involved. |
|