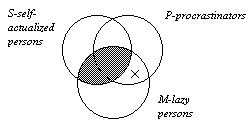| I. A logical analogy is useful to show the invalidity of a
given argument to someone untrained in logic. Often a logical analogy is more rhetorically
effective in everyday life than a demonstration of invalidity. |
|
A. An argument is valid if and only if its conclusion
follows with certainty from its premisses. Since validity is established by the form of an
arguments, all arguments of the same form will have the same status of validity or
invalidity. |
|
B. The effectiveness of a logical analogy depends upon this
characteristic of arguments. If an invalid argument is offered, a logical analogy can
be constructed as follows: |
|
|
1. Invent classes so that the
conclusion is clearly false. For our purposes, we will generally start with the
classes "dogs," "cats," and "animals." |
|
|
2. Substitute the appropriate minor
and major terms in the major and minor premisses. |
|
|
3. Choose a middle term which will
make the premisses clearly true. |
|
C. In this manner, we will create an argument of the same
form with true premisses and a false conclusion. As you remember, this is the only
combination of truth values which cannot occur in a valid argument. |
|
|
1. The inter-related topics of truth, validity, and
soundness are the heart of deductive logic and form the central concepts of the course. |
|
|
2. If these concepts are somewhat hazy to you, please feel
free to review them now: Truth, Validity, and Soundness.
For more information, see also these notes on the concepts. |
|
|
3. The important point to remember here is that true
premisses and a false conclusion can never occur in a valid argument. If we can
construct an analogy with true premisses and a false conclusion, then the given argument
is invalid. |
|
|
|
a. If a syllogism is invalid, then any other syllogism of
the same form is invalid. |
|
|
|
b. If a syllogism is valid, then any other syllogism of the
same from is valid. |
|
D. If the syllogism we are trying to refute is valid, we
cannot, of course, construct a refutation of that argument by means of a logical analogy.
A refutation would be logically impossible. (If a refutation by means of a logical analogy
were possible for a valid argument, then logic would be useless to prove any
conclusion.) |
| II. Let us consider the following argument proposed by a
humanistic psychologist: "Since some procrastinators are lazy and no self-actualized
persons are lazy, it follows then that at least some self-actualized persons are not
procrastinators." |
|
A. Our first task is to set up the syllogism in standard
form and order and label our terms. |
|
|
|
P |
|
M |
|
|
|
Some
[procrastinators] are [lazy persons.] |
|
|
|
S |
|
M |
|
|
|
No
[self-actualized people] are [lazy
persons.] |
|
|
|
S |
|
|
P |
|
|
Some
[self-actualized persons] are not [procrastinators.] |
|
B. The argument was composed by performing these steps. |
|
|
1. Identify the conclusion. |
|
|
2. Identify the minor and major terms. |
|
|
3. Identify the major premiss. |
|
|
4. Identify the minor premiss. |
|
|
5. Label the middle term. |
|
|
6. Complete our labeling as we write out the syllogism in
standard form and order. |
|
C. It's a good idea to sketch out a Venn Diagram of the
argument ahead of constructing the analogy for two reasons. The procedure for doing Venn
Diagrams is explained here: Venn Diagrams. |
|
|
1. The Venn Diagram will show us whether the argument is
valid or not. If the argument is valid, we cannot construct a logical analogy no
matter how long and hard we work. |
|
|
2. The diagram reveals the logical structure of the argument
graphically, so, frequently, the choices for the analogical classes are more easily
chosen. |
|
|
3. Just inventing any false conclusion from which to
substitute into the form of an invalid syllogism might not involve classes which can be
used to mirror the form of the original argument. |
|
D. The diagram for our IEO-4 syllogism is as follows.
It is clearly invalid since we cannot find an "X" in the S-lune.
Until we explain Venn Diagrams more fully, please accept this analysis for the moment. |
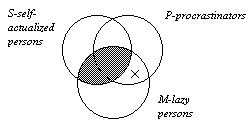 |
|
E. Now that we know the argument is invalid, we can proceed
with our logical analogy. |
|
|
1. Invent a false conclusion. Let's try
"Some dogs are not animals." |
|
|
2. Substitute the minor and major terms in the minor and
major premiss. Since "dogs" is our minor term and "animals" is our
major term, we obtain the following schema. |
|
|
|
Some [animals] are [__________.] |
|
|
|
No [dogs] are [__________.] |
|
|
|
Some [dogs] are not [animals.] |
|
|
3. Invent a middle term so that the premisses are true.
The class "cats" naturally suggests itself. The analogy is completed. |
|
|
4. Rhetorically then a response to the psychologist's
argument could be put in this manner. "You have argued that some self-actualized
persons are not procrastinators because some procrastinators are lazy, and no
self-actualized persons are lazy. But this is just like arguing that some dogs are not
animals because some animals are cats, and no dogs are cats." |
| III. Although logical analogies are useful and effective, we
want to develop more reliable ways to test the validity of syllogisms. The two methods
developed later are the Venn Diagram technique and the Rules of
Validity for Standard Form Categorical Syllogisms. |
|
A. These other techniques are used because sometimes it is
difficult to construct a logical analogy quickly. |
|
B. Also, of course, we cannot refute a valid argument by
means of devising a logical analogy, and we need methods to determine ahead of time
whether a logical analogy can be constructed. |
 Philosophy 103: Introduction to Logic
Philosophy 103: Introduction to Logic