![]()
|
|
|
Homepage > Logic > Symbolic Logic > The Language of Symbolic Logic
| Quizzes |
| Tests |
| FAQ |
| Links |
| Search |
| Readings |
| Archives |
| Syllabus |
 Philosophy
103: Introduction to Logic
Philosophy
103: Introduction to Logic
The Language of Symbolic Logic
Abstract: Conventions for translating ordinary language statements into symbolic notation are outlined.
- We are going to set up an artificial "language" to avoid
difficulties of vagueness, equivocation, amphiboly, and confusion from
emotive significance.
- The first thing is to learn the elements of this "new language."
- The second is to learn to translate ordinary language grammar into symbolic notation.
- The third thing is to evaluate arguments in this "new language."
- The first thing is to learn the elements of this "new language."
- Symbolic logic is by far the simplest kind of logic—it is a great
time-saver in argumentation. Additionally, it helps prevent logical confusion.
- The modern development begin with George Boole in the 19th century.
- Symbolic logic can be thought of as a simple and flexible shorthand:
- Consider the symbols:
[(p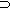 q)
q)  (q
(q 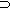 r)]
r)] 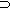 (p
(p 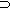 r).
r).
- This rule was well known to the Stoics, but they expressed it this way:
"If, if the first then the second and if the second then the third, then, if the first then the third."
- We will find that all of the essential manipulations in symbolic
logic are about as complex and working with numbers made up of ones and zeros.
- Consider the symbols:
- The modern development begin with George Boole in the 19th century.
- We begin with the simplest part of propositional logic: combining simple propositions into compound propositions and determining the truth value of the resulting compounds.
- Propositions or statements can be thought of as the "atoms" of propositional logic. (“Proposition” and “statement” are often taken to be equivalent terms.)
- Simple propositions are statements which cannot be broken down without a loss in meaning.
- E.g., "John and Charles are brothers" cannot be broken down without a change in the meaning of the statement.
Note the change in meaning with "John is a brother" and
"Charles is a brother."
- Whereas, "John and Charles work diligently" can be broken down without a change in meaning:
"John works diligently." "Charles works diligently." (It is assumed contextually that the meaning of the original statement is not that John and Charles work diligently together but perhaps not so apart.)
- E.g., "John and Charles are brothers" cannot be broken down without a change in the meaning of the statement.
Note the change in meaning with "John is a brother" and
"Charles is a brother."
- Conventionally, capital letters (usually towards the beginning of the alphabet) may be used as abbreviations for specific propositions.
E.g., "John and Charles are brothers" can be symbolized as B.
and "John and Charles work diligently" can be symbolized as J and C.
The logical operator "and," as we will see, will be symbolized as " " .
" .
- Simple propositions are statements which cannot be broken down without a loss in meaning.
- In addition to propositions, propositional logic contains another element: operators on propositions.
- Propositions can be thought of like the sticks of a tinker-toy set.
- Operators are like the connecting blocks.
- By adding more and more operators, we get more complex structures.
- Propositions can be thought of like the sticks of a tinker-toy set.
- For evaluation of statements, there is only one condition to be learned:
"In order to know the truth value of the proposition which results from applying an operator to propositions, all that need be known is the definition of the operator and the truth value of the propositions used."
- Propositions or statements can be thought of as the "atoms" of propositional logic. (“Proposition” and “statement” are often taken to be equivalent terms.)
Send corrections or suggestions to webmaster@philosophy.lander.edu
Read the disclaimer
concerning this page.
12.26.04
© 2004 Licensed under GFDL
Arguments | Language | Fallacies | Propositions | Syllogisms | Translation | Symbolic
![]()
![]()
