
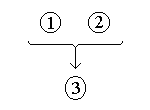
Diagramming Arguments, Premise and Conclusion Indicators, with Many Examples
Abstract: Analyzing the structure of arguments is clarified by representing the logical relations of premises and conclusion in diagram form. Many ordinary language argument examples are explained and diagrammed.
Contents
“Argument” Defined
- The use of the term “argument” in logic is in
accordance with this precising definition; the term is not used
in logic to refer to bickering or contentious disagreements.
Formal arguments are evaluated by their logical structure; informal arguments are studied and evaluated as parts of ordinary language and interpersonal discourse.
- The presence of an argument in a passage is discovered by
understanding the author's intention of proving a statement by
offering reasons or evidence for the truth of some other statement.
Generally speaking, these reasons are presented as verbal reports. The reasons might not always be initially presented in declarative sentences, but in context must have their meaning preserved by translation or paraphrase into a statement or proposition.
close ×Statement or Proposition:
A verbal expression in sentence form which is either true or false (but not both) — i.e., a sentence with a truth value.
- The use of the term “argument” in logic is in
accordance with this precising definition; the term is not used
in logic to refer to bickering or contentious disagreements.
How to Identify the Presence of an Argument
- There are three main ways of judging the presence of an
argument:
- The author or writer explicitly states
the reasons, evidence, justification, rationale, or proof of
a statement.
 Example:
Example:
[1] I conclude the dinosaurs probably had to cope with cancer. These are my reasons: [2] a beautiful lower leg bone was found in Alberta, [3] the end of the fibula was grossly malformed, and [4] this appearance closely matches osteosarcoma in humans.
Usually, however, the emphasized phrases, “I conclude” and “These are my reasons” are omitted in the text for stylistic reasons — leaving the structure of the argument to be inferred from the meanings of the statements used and less obvious transitional phrases which might indicate reasons or conclusions.
- The author uses argument indicators signifying
the presence of an argument.
Example:Since [1] the solution turns litmus paper red, [2] I conclude it is acidic, inasmuch as [3] acidic substances react with litmus to form a red color.
In this argument, “since” is being used as a premise indicator and “conclude” is used as a conclusion indicator, and “inasmuch as” is another premise indicator.
- Ask yourself “What is the author trying to prove
in this passage?” In order to determine whether or
not an argument is present in a passage, it sometimes helps to pose
this question. If an answer is directly forthcoming, then the passage
is most likely an argument.
Despite that, the presence of an argument cannot be always known with certainty; often the purpose of the passage can only be contextually surmised. Establishing the intention of a speaker or writer is sometimes the only determining factor of whether or not an argument is present.
A charitable, and insofar as possible, an impartial conventional interpretation of the context, content, and purpose of the passage should be sought.
- The author or writer explicitly states
the reasons, evidence, justification, rationale, or proof of
a statement.
- What if indicators are not present in a passage?
The identification of arguments without argument indicators present
is achieved by recognizing from the meanings of the sentences themselves
when evidence or reasons are being provided in support of a concluding
statement.
For example, evaluate this passage:“[1] The types of sentences you use are quite varied. [2] I've noticed that your recent essays are quite sophisticated. [3] You have been learning much more about sentence structure.”
Note that if we ask upon reading this passage, “What is being proved?,” then the answer in statement [3] suggests itself as resulting naturally from the first two sentences.
That is, statements [1] and [2] are direct experiential evidence giving reasons for the the truth of the main point (or that which is intended to be proved): namely, the inference to [3] “You have been learning much more about sentence structure.”
So, in the context of a simple argumentative passage, if statements are given as suppositions, observations, or facts without evidence or logical support, those statements are premises. If a statement is given logical or evidential support from another statement or statements, that statement is a conclusion (or subconclusion if the argument is complex).
- There are three main ways of judging the presence of an
argument:
How to Analyze Simple Arguments
In order to analyze simple and complex arguments, we will find it useful to construct a diagram of the structure of the argument that sets forth the relations among the various premises and conclusions.
- The conclusion of one argument can become a premise for another
argument. Thus, a statement can be the conclusion of one argument
and a premise of a following argument — just as a daughter in one
family can become a mother in another family.
For example, consider this argument chain:“Because [1] of our preoccupation with the present moment and the latest discovery, [2] we do not read the great books of the past. Because [3a] we do not do this sort of reading, and [3b] do not think it is important, [4] we do not bother about trying to learn to read difficult books. As a result, [5] we do not learn to read well at all.” [1]
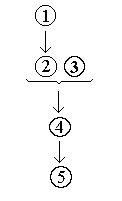 Diagramming the argument illustrates the internal logical structure more
clearly than the written description:
Diagramming the argument illustrates the internal logical structure more
clearly than the written description:
Statement [1] provides evidence for [2].
Next, [2] together with [3] ([3a] and [3b] being combined here as one compound statement for simplification) gives evidence for [4].
Finally, as a result of [4], statement [5] concludes with some degree of probability.
- The number of arguments in a passage is conventionally established
by the number of conclusions in that passage.
- In analyzing the structure of an argument, whether
simple or complex, the all-important first step is to find the
conclusion. Here are some specific suggestions as to how to
find the conclusion.
- The conclusion might be evident from the content and
context of the paragraph structure. The sequence of sentences
is often an indication of the conclusion. Arrangement of
sentences from most general to specific is a common form of
paragraph or passage; the arrangement of sentences from specific
to general is a bit less common.[2] Considering both
cases, the conclusion is often the first or the last
sentence in a passage. [3]
Example argument:[1] John didn't get much sleep last night. [2] He has dark circles under his eyes. [3] He looks tired.
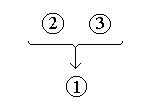 The conclusion is the first sentence in the passage. Statements [2]
and [3] are observational evidence for statement [1] which
is inferred from those observations.
The conclusion is the first sentence in the passage. Statements [2]
and [3] are observational evidence for statement [1] which
is inferred from those observations.
- Nevertheless, the conclusion can occur anywhere in the paragraph,
especially if the passage has not been revised for clarity. Usually,
if a conclusion is not the first or last sentence of an argumentative
paragraph, a conclusion indicator is present, or the last sentence
is presented as an after-thought with a premise indicator. Frequently
used argument indicators are highlighted below in separate boxes under
separate headings.
Example Argument:[1] Studies from rats indicate that neuropeptide Y in the brain causes carbohydrate craving, and [2] galanin causes fat craving. Hence, [3] I conclude that food cravings are tied to brain chemicals [4] because neuropeptide Y and galanin are brain chemicals.
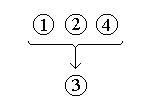
- The structure of the argument can be inferred by attending to
the premise and conclusion indicators even though the content of the
argument might not be fully understood.
- Take care not to rely overly on premise and conclusion indicators
in a “mechanical” automatic analysis without attending to
understanding the argument in question.
Sometimes the final conclusion is not designated by a conclusion indicator, as in the following example:
[1] The piano teacher should consider an additional study of the pipe organ. [2] As an organist. the teacher would have added income at times when she is not teaching; consequently, and for this reason [3] she would receive added publicity and prestige. Therefore, [4] she would be likely to attract additional students and additional income.
The first statement is not merely an introduction to the argument. If you were to identify the main conclusion in this passage by highlighting the premise and conclusion indicators before understanding the import of the argument, it is quite likely the last statement would be selected as the main point of the argument. However, if you begin the analysis by reading for understanding, the first statement should stand out as the central point of the passage.
Consequently, in all argument analyses, be sure to consider first the overall meaning of the passage in order to identify its ultimate conclusion.
- The conclusion might be evident from the content and
context of the paragraph structure. The sequence of sentences
is often an indication of the conclusion. Arrangement of
sentences from most general to specific is a common form of
paragraph or passage; the arrangement of sentences from specific
to general is a bit less common.[2] Considering both
cases, the conclusion is often the first or the last
sentence in a passage. [3]
- The conclusion of one argument can become a premise for another
argument. Thus, a statement can be the conclusion of one argument
and a premise of a following argument — just as a daughter in one
family can become a mother in another family.
Working with Premise Indicators:
Premise indicators are terms which often signal and precede the presence of reasons. Frequently used premise indicators include the following terms:for
since
as
because [* when the term means “for the reason that” but not when it means “from the cause of”]
in as much as
follows from
after all
in light of the fact
assuming
seeing that
granted that; given that
in view of
as shown by; as indicated by
deduced from
inferred from; concluded from
due to the fact that
for the reason [* often mistaken for a conclusion indicator]
- Examples of their use in arguments:
- “[1] The graphical method for solving a system of
equations is an approximation, since [2] reading the
point of intersection depends on the accuracy with which the
lines are drawn and on the ability to interpret the coordinates
of the point.”
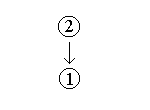 The term “since” indicates that the second clause
of this passage is a premise, the first clause is left as the
conclusion.
The term “since” indicates that the second clause
of this passage is a premise, the first clause is left as the
conclusion.
In practice, the second clause can be broken down into two separate premises so that the argument could have also have been set up as follows:
So under this interpretation, [2a] together with [2b] is evidence for [1].[2a] Reading the point of intersection of a graph depends on the accuracy with which the lines are drawn.
[2b] Reading the point of intersection also depends upon the ability to interpret the coordinate of the point.
[1]Thus, the graphical method for solving a system of equations is an approximation.
- A simpler argument with a premise indicator:
 [1] Questionable research practices are far more common than
previously believed, after all, [2] the Acadia Institute
found that 44 percent of students and 50 percent of faculty from
universities were aware of cases of plagiarism, falsifying
data, or racial discrimination.
[1] Questionable research practices are far more common than
previously believed, after all, [2] the Acadia Institute
found that 44 percent of students and 50 percent of faculty from
universities were aware of cases of plagiarism, falsifying
data, or racial discrimination.
- “[1] The graphical method for solving a system of
equations is an approximation, since [2] reading the
point of intersection depends on the accuracy with which the
lines are drawn and on the ability to interpret the coordinates
of the point.”
- Try the following examples for yourself:
- “[1] [I]t seems hard to prove that the composition of music and words was ever a simultaneous process. [2] Even Wagner sometimes wrote his ‘dramas’ years before they were set to music; and, [3] no doubt, many lyrics were composed to fit ready melodies.” [4]
 Although there are no indicators for the first two statements
in this passage, the second two statements are examples which
support or give evidence for the first more general statement.
The word “and” connects clauses of equal status.
Therefore, the first statement is the conclusion of the argument.
Although there are no indicators for the first two statements
in this passage, the second two statements are examples which
support or give evidence for the first more general statement.
The word “and” connects clauses of equal status.
Therefore, the first statement is the conclusion of the argument.
This is a weak inductive argument: the conclusion is supported by only one example.
- “[1] [A]ny kind of reading I think better than leaving a blank still a blank, [2] because the mind must receive a degree of enlargement and [3] obtain a little strength by a slight exertion of its thinking powers.”[5]
 The premise indicator “because” indicates the first
premise. Note that the “and” before the last clause [3]
in this passage connects clauses of equal standing; so [3] should be
tacitly understood as this independent clause:
The premise indicator “because” indicates the first
premise. Note that the “and” before the last clause [3]
in this passage connects clauses of equal standing; so [3] should be
tacitly understood as this independent clause:
“[3] [the mind must] obtain a little strength by a slight exertion of its thinking powers.”
The conjunction “and” connects statements of equal status, so since [2] is a premise, the statement following it is also a premise — that leaves the first statement as the conclusion of this argument.
Argument reconstruction of this kind is often done for clearer understanding of the reasoning prior to evaluation. (This argument is inductive since the conclusion does not follow with certainty.)
- Examples of their use in arguments:
Working with Conclusion Indicators:
Conclusion indicators are words which often signal and precede the statement which logically follows from the reasons given. Common conclusion indicators include the following:thus
therefore
consequently
hence
so
it follows that
proves that; demonstrates that; shows that
indicates that
accordingly [* an indicator often missed]
implies that; entails that; follows that
this means
we may infer; it can be inferred that
suggests that
results in
in conclusion
for this reason; for that reason [* often mistaken for premise indicators (a conclusion follows these phrases; a premise precedes these phrases.)]
- Examples of conclusion indicator use in arguments:
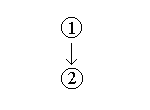 [1] No one has directly observed a chemical bond, [2] so
scientists who try to envision such bonds must rely on experimental
clues and their own imaginations.
[1] No one has directly observed a chemical bond, [2] so
scientists who try to envision such bonds must rely on experimental
clues and their own imaginations.
 [1] Math grades for teens with bipolar disorder usually drop
noticeably about one year before their condition is diagnosed,
thus [2] probably bipolar disorder involves a deterioration
of mathematical reasoning.
[1] Math grades for teens with bipolar disorder usually drop
noticeably about one year before their condition is diagnosed,
thus [2] probably bipolar disorder involves a deterioration
of mathematical reasoning.
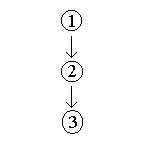
- [1] Coal seams have been discovered in Antarctica. [2] This
means that the climate there was once warmer than it is now.
[3] Thus, either the geographical location of the continent
has shifted or the whole Earth was once warmer than it is now.

- Try the following diagramming examples for yourself:
- “[1] We humans appear to be meaning-seeking creatures who have had the misfortune of being thrown into a world devoid of meaning. [2] One of our major tasks is to invent a meaning sturdy enough to support a life and [3] to perform the tricky maneuver of denying our personal authorship of this meaning. [4] Thus we conclude instead that it [our meaning of life] was ‘out there’ waiting for us.” [6]
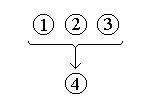 The only indicator in the argument is the conclusion indicator
“Thus” in statement [4]. The first two sentences
are divided here into three statements which provide the reasons
for concluding statement [4].
The only indicator in the argument is the conclusion indicator
“Thus” in statement [4]. The first two sentences
are divided here into three statements which provide the reasons
for concluding statement [4].
(It would have been acceptable also to interpret the sentence beginning with [2] as one statement. If this whole argument were related to other arguments, the choice of how to divide up the statements would be made by translations which best match the related ideas.)
The central idea of the passage is that since [the author thinks] life has no intrinsic meaning, to live well we must invent a meaning for our lives and then believe this imposed meaning is genuinely real.
- ”[1] The fact is that circulating in the blood of the organism, a carcinogenic compound undergoes chemical changes. [2] This is, for instance, the case in the liver, which is literally crammed with enzymes capable of inducing all sorts of modifications. So [3] it may well be that cancer is induced not by the original substances but by the products of their metabolism once inside the organism.” [7]
 The only indicator is the conclusion indicator “So” in
statement [3]. The first two statements describe a fact and an example
which indicate by induction the final concluding generalization [3].
The only indicator is the conclusion indicator “So” in
statement [3]. The first two statements describe a fact and an example
which indicate by induction the final concluding generalization [3].
Notice that statement [3] could have been interpreted as two statements:“[3a] So it may well be that cancer is induced not by the original substances but [3b] [it may well be that cancer is induced] by the products of their metabolism once inside the organism.”
However, in this case, it seems clearer to keep [3a] and [3b] as one statement since [3a] and [3b] express one complete thought. Either interpretation is possible; the simpler one is taken here.
- Examples of conclusion indicator use in arguments:
Working with Equal Status Indicators:
Indicators of Equal Status of Premises or Conclusions: Conjunctives (including some conjunctive adverbs) often indicate equal status of premise or conclusion in connecting clauses or sentences. Noticing these conjuncts is especially helpful in argument analysis. Indicators of clauses of equal status also include certain adverbial clauses, “conditional, concessive, and contrastive terms,” informing of some type of expectation or opposition between clauses:or [the inclusive “or,” i.e. “either or or both”]
and
as [* when it connects similar clauses; not when it connects a result with a cause]
in addition
although
despite; in spite of
besides
though
but
yet
however
moreover
nevertheless
not only … but also
(and also the semicolon “;”)
- If one of the clauses has already been identified as a premise
or a conclusion of an argument, then its coordinating clause is
probably the same type of statement. Check the following examples.
- The equal status indicator “and”:
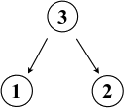
![Argument diagram shows statements
[2] and [3] lead to statement [1]. Argument diagram shows statements
[2] and [3] lead to statement [1].](images/diagram_23-1.gif) [1] Some students absent today are unprepared for this test,
since [2] the law of averages dictates that only 10% of
students are absent due to illness, and [3] more than
10% are absent.
[1] Some students absent today are unprepared for this test,
since [2] the law of averages dictates that only 10% of
students are absent due to illness, and [3] more than
10% are absent.
Comment: Notice that statements [2] and [3] work together as a reason, so both together provide evidence for [1].
Having separate arrows for [2] and [3] leading to conclusion [3] would represent a misunderstanding of the argument.
- The equal status indicator “not only …
but also.”
![Argument diagram shows premise [1]
leads to conclusions [2] and [3]. Argument diagram shows premise [1]
leads to conclusions [2] and [3].](images/diagram_1-23.gif) [1] Lenses function by refracting light at their surfaces.
Consequently, not only [2] does their action depends
on the shape of the lens surfaces but also [3] it
depends on the indices of refraction of the lens material and
the surrounding medium.
[1] Lenses function by refracting light at their surfaces.
Consequently, not only [2] does their action depends
on the shape of the lens surfaces but also [3] it
depends on the indices of refraction of the lens material and
the surrounding medium.
Comment: Notice that sentence [3] could have been divided into two statements as follows:“ … [3] it depends on the indices of refraction of the lens material and [4] [it depends on] the surrounding medium.”
(Again, how sentences should be divided into different statement depends, to a large degree, on how the argument under analysis is related to any other contextual statements and arguments.)
- Try the following examples for yourself:
 We could simply consider [1] and [2] as one statement, but
the argument seems be clearer to consider [2] as elliptically
expressing the statement “[2] [Mystery is] unscientific.”
The premise indicator “since” identifies the only
premise.
We could simply consider [1] and [2] as one statement, but
the argument seems be clearer to consider [2] as elliptically
expressing the statement “[2] [Mystery is] unscientific.”
The premise indicator “since” identifies the only
premise.
- “[1] Many of those children whose conduct has been most narrowly watched, become the weakest men, because [2] their instructors only instill certain notions into their minds, that have no other foundation than their authority; and [3] if they be loved or respected, the mind is cramped in its exertions and wavering in its advances.” [9]
 The premise indicator “because” indicates the first
premise connected by the equal status connector “and”
which identifies the second premise. By elimination, then first
independent clause is the conclusion.
The premise indicator “because” indicates the first
premise connected by the equal status connector “and”
which identifies the second premise. By elimination, then first
independent clause is the conclusion.
 “For [1] there is altogether one fitness (or harmony). And [2] as the universe is made up out of all bodies to be such a body as it is, so [3] out of all existing causes necessity (destiny) is made up to be such a cause as it is.” [10]
“For [1] there is altogether one fitness (or harmony). And [2] as the universe is made up out of all bodies to be such a body as it is, so [3] out of all existing causes necessity (destiny) is made up to be such a cause as it is.” [10]
 The argument is clearly marked with indicators:
The argument is clearly marked with indicators:
For [1] and [2], so [3].
The initial premise indicator “for” connects its clause [1] to the next clause of equal standing [2] by means of the equal status indicator “and.” Finally, the conclusion [3] is marked by the conclusion indicator “so.”
- If one of the clauses has already been identified as a premise
or a conclusion of an argument, then its coordinating clause is
probably the same type of statement. Check the following examples.
How to Analyze Complex Arguments
When analyzing complex arguments, it can be helpful to reconstruct the argument by identifying the main conclusion first, and then by working backwards, locate the premises by any premise indicators present.
- Consider the following argument:
[1] If students were environmentally aware, they would object to the endangering of any species of animal. [2] The well-known Greenwood white squirrel has become endangered [3] as it has disappeared from the Lander campus [4] because the building of the library destroyed its native habitat. [5] No Lander students objected. [6] Thus, Lander students are not environmentally aware.
Note that the following indicators are given in this passage:as
The argument is complex:
because
thus
- Statement [6] is the final conclusion since it has the conclusion
indicator “thus” and the import of the paragraph indicates
that this statement is the main point of the argument. (It is also the
last sentence in the paragraph.)
 The premise indicators suggest that [2] is a subconclusion
of [3] since the indicator “as” connects them, and [3],
in turn, is a subconclusion of [4] since the indicator
“because” connects those two statements.
The premise indicators suggest that [2] is a subconclusion
of [3] since the indicator “as” connects them, and [3],
in turn, is a subconclusion of [4] since the indicator
“because” connects those two statements.
- The only statements not yet examined are [1] and [6].
After a bit of thought, the structure of the first statement [1] considered together with statement [5] should suggest itself as a common argument form:[1] If students were environmentally Aware, [then] they would Object to the endangering of any species of animal.
which can be abbreviated as follows:
[5] No student Objected [to the endangering of the Greenwood white squirrel].
The negation of the consequent clause O by the second premise leads us to expect the conclusion “Not A”.[1] If A then O
[5] Not O
Aha! “Not A” is the same thing as the conclusion [6] we identified in step 1:“[6] Thus, Lander students are not environmentally Aware,”
(Later in the course we will see that this often used argument structure is termed modus tollens.)
So the diagram of this internal sub-argument then is as follows:
(Note that “Not A” is the same statement as [6].)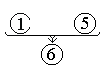
[1] If A then O
[5] Not O
[6] Not A
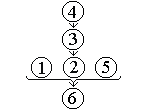 Hence the whole argument can now be pieced together as the following
complex argument:
Hence the whole argument can now be pieced together as the following
complex argument:
- Statement [6] is the final conclusion since it has the conclusion
indicator “thus” and the import of the paragraph indicates
that this statement is the main point of the argument. (It is also the
last sentence in the paragraph.)
- Caution: In same contexts, the use of indicator words such as
those listed above do not typically indicate the presence of an argument.
For instance, “because” and “so” are used as indicator
words in explanations; “since” and “as” are very
often used in other contexts than argumentation also.
Consider this passage:“The explanation as to why productivity has slumped since 2004 is a simple one. That year coincided with the creation of Facebook”[11]
The passage here is probably intended to amuse rather than explain why productivity has slumped. The explanation also has cogency as an argument, as well. In cases like this, the import of the passage can only be determined from its context. (Notice that “since” in the above argument is used as a preposition, not as a conjunctive adverb used as a premise indicator. And “as” is being used in the sense of “in the way that” rather than that of connecting clauses of similar or equal status.)
So, the presence of words in our argument indicator lists is not a sure sign an argument is present. The grammar of the passage need be considered. Here are two examples of passages where it's doubtful that the writer intended to offer an argument:
 Literary Implication: For example, in the following book
review, two prose images drawn from the work of the poet
Stevie Smith are used to illustrate a literary insight.
Literary Implication: For example, in the following book
review, two prose images drawn from the work of the poet
Stevie Smith are used to illustrate a literary insight.
In the passage excerpted below, the emphasized phrase “The implication … is” does not function as an argumentative conclusion indicator. Instead, the prose images are intended to suggest a meaning beyond the literal interpretation of the events pictured:“In The Voyage of the Dawn Treader, the ship's prow is ‘gilded and shaped like the head of a dragon with wide open mouth’ so when, a moment later, the children stare at the picture ‘with open mouths’, they are being remade in its image … The painted ocean to which Joan is drawn is ‘like a mighty animal’, a ‘wicked virile thing’. The implication in both cases is that art is not safe, and that this is why it's needed.” [emphasis mine] [12]
From a logical point of view, literary implication is a type of imaginative generalization meant to enlighten rather than provide evidence or demonstrate a conclusion.
- So it's important to realize that the presence of terms in the
argument indicator lists is not a sure sign the passage is an argument
— these words are very often used in other contexts. The use of
these terms are determined within the contexts in which they appear.
By way of example, evaluate this passage from the Hindu texts of the Upanishads:
Evaluated superficially, this passage could be analyzed as a circular argument“He asked: ‘Who are the Âdityas?’
Yâgñavalkys replied: ‘The twelve months of the year, and they are Âdityas, because they move along (yanti) taking up everything [i.e., taking up the lives of persons, and the fruits of their work] (âdadânâh). Because they move along, taking up everything, therefore they are called Âdityas.’”[emphasis mine][13]
— but in context, the purpose of the passage is merely to define and explain the meaning of the word “Âdityas.”close ×Circular Argument:
Also termed “begging the question” or “petitio principii,” the argumentative fallacy of assuming in a premise the same statement which was to be proved. Formally the argument is valid, but is considered by some logicians fallacious when deceptive.
- Consider the following argument:
Links to Diagramming Online Quizzes with Suggested Solutions
Test your understanding with any of the sections for diagramming on the following quizzes, tests, or exercises:Quiz: Diagramming Simple Arguments
Problem Set 1 PDF
Problem Set 2 PDF
Problem Set 3 PDF
Test: Structure of Arguments Part I
postscript
“There is however a method for extracting arguments and setting out their structure. This is how it goes. First go through the text circling the inference indicators “thus” “therefore” etc. Next identify the main conclusion of the argument and underline it. Then look for the reasons given to support that conclusion and place them in angle (brackets). Now iterate the following procedure for as long as possible. Take a (reason) and look for reasons given to support it. If you find any, then underline the (reason) which is now also a conclusion. When the process terminates the (reasons) that are not underlined are the premisses to the argument, the (reasons) underlined are intermediate conclusions.”Peter Mott, review of The Logic of Real Arguments, by Alec Fisher, The Philosophical Quarterly 39 no. 156 (July, 1989), 370-373.
Notes: Diagramming Arguments
1. Mortimer J. Adler, How to Read a Book (New York: Simon and Schuster: 1940), 89. ↩
2. Some English textbooks describe argumentative paragraph structure as deductive (proceeding from general to specific statements or inductive (proceeding from specific to general statements). For example, educator and rhetorician Fred Newton Scott writes:
“There are two orders of progress in thought, one proceeding from the statement of a general principle to particular applications of the principle (deductive reasoning), the other proceeding from the statement of particular facts to a general conclusion from those facts (inductive reasoning). In deductive reasoning, the general principle (stated usually at the beginning) is applied in the particulars; in inductive reasoning the general principle (stated usually at the end) if inferred from the particulars, as a conclusion. In a deductive paragraph, as would be expected, the sentences applying the principle to the particular case in hand, usually follow the topic-statement, which announces the principle. In an inductive paragraph the sentences stating the particular facts usually precede the topic-statement, which gives the general conclusion.” [emphases deleted]
Fred Newton Scott, Paragraph-Writing (Boston: Allyn and
Bacon, 1909), 62-63.
Since this distinction between induction and
deduction proves faulty for many arguments, deductive arguments
are now described as those that provide total support for their conclusion
(i.e.,a they logically entail the conclusion); whereas, an inductive
argument give partial support for their conclusion (i.e., they
provide only some evidence for the conclusion.)↩
3. Most paragraphs have a three-part structure: introduction (often a topic sentence), body (often supporting sentences), and conclusion (often a summary statement). In argumentative writing, the conclusion of an argument is often the topic sentence or main idea of a paragraph. Consequently, the first sentence or last sentence of many argumentative paragraphs contain the conclusion.↩
4. René Wellek and Austin Warren, Theory of Literature (New York: Harcourt, Brace: 1956), 127.↩
5. Mary Wollstonecraft, Vindication of the Rights of Woman (1792 London: T. Fisher Unwin, 1891), 273.↩
6. Irvin D. Yalom, The Gift of Therapy (New York: Harper Perennial, 2009), 133.↩
7. Maxim D. Frank-Kamenetskii, Unraveling DNA trans. Lev Liapin (New York: VCH Publishers, 1993), 175.↩
8. Bertrand Russell, The Analysis of Mind (London: 1921 George Allen & Unwin, 1961), 40. ↩
9. Wollstonecraft, Vindication, 175.↩
10. Marcus Aurelius, Meditations, trans George Long (New York: Sterling: 2006), 69.↩
11. Nikko Schaff, “Letters: Let the Inventors Speak,” The Economist 460 no. 8820 (January 26, 2013), 16.↩
12. Matthew Bevis, “What Most I Love I Bite,” in the “Review of The Collected Poems and Drawings of Stevie Smith,” London Review of Books 38 No. 15 (28 July 2016), 19.↩
13. Brihadâranyaka-Upanishad in The Upanishads, Pt. II, trans. F. Max Müller in The Sacred Books of the East, Vol. XV, ed. F. Max Müller (Oxford: Clarendon Press, 1900), 141.↩
Readings: Diagramming Arguments
Carnegie Mellon University, iLogos: Argument Diagram Software and User Guide Free software cross-platform. Also, a list with links to other argument diagramming tools.
Martin Davies, Ashley Barnett, and Tim van Gelder, “Using Computer-Aided Argument Mapping to Teach Reasoning,” in Studies in Critical Thinking, ed. J. Anthony Blair (Windsor, ON: Open Monograph Press, 2019), 131-176. Chapter outlining how to use argument mapping software in logic classes. doi: 10.22329/wsia.08.2019
Jean Goodwin, “Wigmore's Chart Method,” Informal Logic 20 no. 3 (January, 2000), 223-243. doi: 10.22329/il.v20i3.2278 Tree diagram method for complex argument representation and inference strength assessment for legal analysis.
Mara Harrell, Creating Argument Diagrams, Carnegie Mellon University. Tutorial on identification of indicators, rewriting statements, providing missing premises, and reconstruction of arguments. (28 pp.)
Dale Jacquette, “Enhancing the Diagramming Method in Logic,” Argument: Biannual Philosophical Journal 1 no. 2 (February, 2011), 327-360. Also here. An extension of the Beardsley diagramming method for disjunctive and conditional inferences as well as other logical structures.
Michael Malone, “On Discounts and Argument Identification,” Teaching Philosophy 33 no. 1 (March, 2010), 1-15. doi: 10.5840/teachphil20103311 Discount indicators such as “but”, “however”, and “although” are distinguished from argument indicators, but help in argument identification.
Jacques Moeschler, “Argumentation and Connectives,” in Interdisciplinary Studies in Pragmatics, Culture and Society, eds. Alessandro Capone and Jacob L. Mey (Cham: Springer, 2016), 653-676.
John Lawrence and Chris Reed, “Argument Mining: A Survey,” Computational Linguistics 45 no. 4 (September, 2019), 765-818. doi: 10.1162/coli_a_00364 Review of recent advances and future challenges for extraction of reasoning in natural language.
Frans H. van Eemeren, Peter Houtlosser, and Francisca Snoeck Henkemans, Argumentative Indicators in Discourse (Dordercht: Springer, 2007). Sophisticated study of indicators for arguments, dialectical exchanges, and critical discussion. doi: 10.1007/978-1-4020-6244-5
Wikipedia contributors, “Argument Map, Wikipedia. History, applications, standards, and references for argument maps used in informal logic.
(Free) Online Tutorials with Diagramming
Carnegie Mellon University, Argument Diagramming v1.5 (Open + Free). Free online course on argument diagramming using built-in iLogos argument mapping software by Carnegie Mellon's Open Learning Initiative. (With or without registration and two weeks for completion).
Joe Lau, “Argument Mapping ” Module A10 on the Critical Thinking Web at the University of Hong Kong. (No registration and an hour to complete).
Read the disclaimer concerning this page.
1997-2025 Licensed under GFDL and Creative Commons 3.0


The “Copyleft” copyright assures the user the freedom to use,
copy, redistribute, make modifications with the same terms.
Works for sale must link to a free copy.
The “Creative Commons” copyright assures the user the freedom
to copy, distribute, display, and modify on the same terms.
Works for sale must link to a free copy.

