philosophy.lander.edu       Title: Introduction to Logic

Homepage > Logic > Categorical Syllogisms > Syllogistic Fallacies  > Existential Fallacy     

   
 

Logic Homepage

 

Quizzes
Tests
Links
Search
Readings
Syllabus

 

 

       FALLACY NAVIGATOR        

Introduction to Logic
Syllogistic Fallacies: Existential Fallacy

Abstract: The Existential Fallacy occurring in syllogistic arguments is defined and illustrated with examples.

  1. The final fallacy of the syllogistic fallacies can be illustrated by the following argument:


    “Since no rigid levers are flexible things, Some rigid levers are not elastic bars because all elastic bars are flexible things.”


    1. When set up in standard form and order, the syllogism looks like this:


      All [elastic bars] are [flexible things].

      No [rigid levers] are [flexible things].

      Some [rigid levers] are not [elastic bars].



      1. The Venn Diagram for this argument raises some interesting issues. How would you evaluate the following argument?

        If the argument is valid, you should be able to “read off” the conclusion of the above syllogism as “Some [rigid levers] are not [elastic bars].”

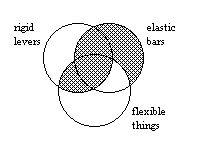
        Diagram of AEO-2 Syllogism




      2. According to our interpretation of the symbols used in Venn diagrams, we would have to have an “X” in the S M P area (i.e., the area of the "rigid levers" class with no marking), but there is no “X”; there. The lack of marking indicates no information is known about that area.

      3. If we had independent information concerning the existence of rigid levers, we would know that at least one rigid lever existed, and this one would have to be in the S M P area of the diagram — the area of the S class with no shading.

      4. However, if we are evaluating the argument as given and we do not assume anything else, we cannot validly get to the conclusion from these premisses, because we cannot see the presence of an “X” outside of the “P” class (i.e., the class of “elastic bars”).


      5. This means on the Boolean interpretation of syllogisms, the subject terms of universal statements are not known to actually exist unless some kind of additional information is provided to the contrary. The Boolean postulation is taken so we can reason about such things as theoretical, imaginary, or fictional entities.

        For example, it is true in Euclidean geometry that “All straight lines are the shortest distance between two points” even though such lines have no width.

        Just as something that has no width does not exist in the everyday world, so also rigid levers (levers that do not distort under any amount of force) do not exist in the everyday world. Perfectly rigid levers are an ideal or theoretical conception of a lever considered as a limiting concept in physics.


    2. On the Boolean interpretation of categorical syllogisms, we cannot assume the existence of individuals mentioned in universal statements. In syllogistic language, if we want to assert that individuals exist, we must say so by adding a particular statement.


      1. On this convention, the word “some” when used in a particular statement is taken to imply at least one individual in the class exists.

      2. In sum, then, on this interpretation, universal statements do not imply either that the classes mentioned or that the members of the classes exist, whereas particular statements do imply that at least one member of the classes mentioned exist.

      3. We take this interpretation in our logic here so that arguments can be presented concerning subjects such as abstract, ideal, or theoretical entities — entities such as frictionless planes, ideal gases, and black bodies which absorb all radiation.


  2. Rule (The Boolean Interpretation): No valid standard form categorical syllogism with a particular conclusion can have both premisses universal.


    1. Reason: If the rule were not followed, then we would mistakenly reason from premisses with no existential import in an attempt to prove a conclusion that does have existential import.


      1. The Existential Import of a statement is established by whether or not its subject exists.

        So, for example, the statement “All persons are mortal beings” is said in ordinary conversation to have existential import because it is common knowledge that persons exist, whereas the statement “All round squares are rhombi” does not have existential import since round squares are known not exist.

      2. We want to be able to reason using terms “referring” to nonexistent things (such as events before the Big Bang, the world in the next century), subjects not known to exist (other universes, ESP, past lives) or surmised subjects (possible worlds, “reasonable men” as a legal fiction, novelist Sinclair Lewis' literary character named “Babbit”) or abstract subjects known not to exist (e.g., nothingness, not-being, emptiness).

      3. A related sense of an existential fallacy in philosophy is illustrated by Søren Kierkegaard's implication in the context of any attempt to prove the existence of God. The existence of the reference of a term does not suddenly emerge from a concluding statement in a logical argument — it would be as if we were attempting to conjure up the existence of God from the presence of written statements on a piece of paper.

      4. Venn Diagrams are used to illustrate the problem of existential import in the example syllogism EAO-4 on this site's page: Venn Diagrams: Categorical Syllogisms.


    2. In sum, the Existential Fallacy occurs whenever a standard form syllogism has two universal premisses and a particular conclusion.



    3. See if you can determine merely by inspection whether or not the following syllogisms commit the Existential Fallacy.

      That is, which of the following syllogisms have two universal premisses with a particular conclusion?


      AAI-3
      		EEO-4
      EAO-1
      		EAI-3
      AE0-1
      		AEA-2
      E00-2
      		AOI-3
      OEO-4
      		OOO-1


    4. Note: If you are using a syllogistic logic presupposing existence, you cannot simply discard this rule against the existential fallacy without adding additional other rules, since the remaining rules on the Boolean interpretation do not rule out all fallacious syllogisms. In other words, the rule against the commission of the existential fallacy prevents other invalid syllogisms as well.


Readings: Existential Fallacy

Raul Corazzon, “The Concept of Existence: Definitions by Major Philosophers“ The webpage excerpts various notions of existence used in the history of philosophy.

“Does This Syllogism by Russell Show That Aristotelian Logic Doesn't Work,” Philosophy Stack Exchange: A discussion about Bertrand Russell's example criticism of Aristotle's syllogisms with this argument:
“If I were to say: ‘All golden mountains are mountains, all golden mountains are golden, therefore some mountains are golden,” my conclusion would be false, though in some sense my premisses would be true.”

Bertrand Russell, “Aristotle's Logic,” in A History of Western Philosophy (1946 London: Taylor and Francis, 2005), 190.

Laurence R. Horn, “All John's Children are as Bald as the King of France: Existential Import and the Geometry of Opposition,” Chicago Linguistic Society 33 (1997), 154-179. A thorough discussion of the traditional and modern views of existential import and related topics for the square of opposition and the four kinds of categorical propositions.

Gyula Klima, “Existential Import and the Square of Opposition,” in John Buridan (Oxford: Oxford University Press, 2009), 143-157. doi: 10.1093/acprof:oso/9780195176223.003.0006

Terence Parsons, “The Traditional Square of Opposition: Later Developments,” The Stanford Encyclopedia of Philosophy (Summer, 2017).

Stephen Read, “Aristotle and Łukasiewicz on Existential Import.” Read argues that Aristotle's syllogistic admits empty terms in the square of opposition.

Maria Reicher, “Nonexistent Objects,” The Stanford Encyclopedia of Philosophy (Winter, 2016). Reicher examines the questions which arise from the admission that there are nonexistent objects.

Bertrand Russell; Hugh MacColl, “The Existential Import of Propositions,” Mind New Series 14 no. 55 (July, 1905), 392-402. doi: 10.1093/mind/xiv.3.398 A discussion of the meaning of existence with respect to the existential import of propositions in reference to standard form categorical propositions. MacColl maintains the null-class is a class of non-existences having many unreal members, whereas Russell maintains there is no class of non-existences but only a non-existent class with no members.

Abraham Wolf, The Existential Import of Categorical Predication (Cambridge University Press, 1905).

Michael Wreen, “Existential Import,” Crítica: Revista Hispanoamericana de Filosofía 16 no. 47 (August, 1984), 59-64.

Joseph S. Wu, The Problem of Existential Import (From George Boole to P.F. Strawson) Notre Dame Journal of Formal Logic 10 no. 4 (October 1969), 415-424. DOI: 10.1305/ndjfl/1093893792

       

  

Send corrections or suggestions to larchie[at]philosophy.lander.edu
Read the disclaimer concerning this page.
1997-2020 Licensed under GFDL and Creative Commons 3.0



The “Copyleft” copyright assures the user the freedom to use, copy, redistribute, make modifications with the same terms. Works for sale must link to a free copy.

The “Creative Commons” copyright assures the user the freedom to copy, distribute, display, and modify on the same terms. Works for sale must link to a free copy.

 

Arguments | Language | Fallacies | Propositions | Translation | Symbolic