Syllogistic Fallacies: Fallacy of the Undistributed Middle Term

Syllogistic Fallacy 2:
The Fallacy of the Undistributed Middle Term

Abstract: The syllogistic Fallacy of the Undistributed Middle Term is explained and illustrated with examples.

Fallacy of the undistributed middle term is a formal fallacy committed in standard form syllogisms whenever the term appearing in both premises is undistributed. (I.e., each of middle terms refers to some but not all of the individuals in the premise statements.)

Example of a distributed and undistributed term: In the statement …
All [persons]^D are [primates].^U
…the subject term “persons” is said to be a distributed term since it refers to, or denotes, each and every person.
1. The predicate term “primates” is said to be undistributed since it does not refer to each and every primate — “primates” in that sentence only makes reference to those individuals who are “persons” and not to other kinds of individuals such as as lemurs or gorillas.
  
  [If you want to review the topic of the distribution of subject and predicate terms in categorical statements, here's the link: Distribution of a Term.]
2. The “undistributed middle” is the second fallacy in our list of syllogistic fallacies.
Example of the Fallacy of an Undistributed Middle Term: In the following argument, the only persons likely to approve of the reasoning are those who are focusing only on the truth of the premises and not the structure of the argument:

All [modern feminists]^D are [social equality seekers].^U
All [protofeminists]^D are [social equality seekers].^U
All [protofeminists]^D are [modern feminists].^U

The Venn Diagram is sketched like this:
1. The blank space in the class of “protofeminists” which is outside of the class of “modern feminists” (indicated by the arrow) represents nothing is known about possible individuals existing in this area. Consequently, the premises allow for the possibility that some protofeminists are not in the class of “modern feminists.” Thus, the conclusion …
  “All protofeminists are modern feminists”
  … has not been deductively proved.
2. Intuitively, it is fairly evident that for the conclusion to follow validly, one would have to falsely presuppose the converse major premise …
  “All social equality seekers are modern feminists”
  … (not the originally given “All modern feminists are are social equality seekers”). So if the given major premise were to be converted in this manner, the subject class “social equality seekers” would become distributed.
  
  close ×
  Distribution:
  
  A term is distributed if in the context of the statement it refers to each and every member of the class it denotes; otherwise, the term is said to be undistributed.
3. So, with the major premise converted, the validity of the argument can be illustrated by visualizing how the new argument nests its terms:
  protofeminists ⊳ social equality seekers ⊳ modern feminists[1]
  However, we know from the meaning of the terms used, not all social equality seekers are feminists. So, since this premise if false, the revised argument, although valid, is not a sound
  
  close ×
  Sound Argument
  
  A sound argument is a valid argument with true premises. (And, therefore, of course, the conclusion is necessarily true also.)
  
  argument.
4. In conclusion, in the original argument given above in the lightly shaded box, the class “social equality seekers” is undistributed in both premises since each appears in the predicate of an A statement. Since the middle term is undistributed in both premises, the argument commits the undistributed middle fallacy.

The Fallacy of the Undistributed Middle Term occurs when the middle term is undistributed in both premises.

Corresponding Rule: In a valid standard form categorical syllogism, the middle term must be distributed in at least one premise.
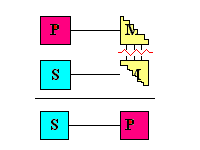Reason: for the two terms of the conclusion to be connected through the third, as in the mechanism shown here, at least one term must be related to the whole of the class designated by the middle term.

Otherwise, the connection might be with different parts of the middle term, as illustrated in the diagram above, and no connection can be made from S to P since the middle term could be referring to nothing in common between the two premises.

John Buridan, a fourteenth century logician, explained the reason for this rule in this manner:
Since the middle is not distributed in either [premise] it is possible that its conjunction with the major extreme is true for one thing and its conjunction with the minor is true for another; and from this no conjunction of the extremes with one another can be inferred …[2]
The premises can related to each other only if at least one of the middle terms is distributed.
In the history of logic, occasionally, an undistributed middle term has been considered an example of equivocation (fallacia æquivocationis) presumably because the denotation of the terms are different since the references of the terms are not necessarily identical in the context of their use.[3]
Note: Remember for the Fallacy of the Undistributed Middle Term to occur, the middle term must be undistributed in both premises, not just one premise.

Optional Exercises: Try these challenging exercises. I think you'll find the mental mastery obtained from the effort well worthwhile.

Try to picture in your mind the position and resultant distribution of the middle terms from the following syllogistic mood and figures without writing them down.

Reminder: The position of the middle term is described by the figure of the syllogism. The figures are named “1,” “2,” “3,” and “4.” They are easily remembered because they form the shape of a flying brick or very wide “W”.

Diagram of the figures of a syllogism.

Think of the middle four Ms on the corners of the orange square representing the empty space between figures 2 and 3.

(1) Visualize the position of the middle term in the following syllogistic forms without writing the three statements in standard form syllogisms.

(2) Then picture in your mind the distribution status of the two statements by the kind of statements used (i.e., an A, E, I, or O,).

(3) State whether or not the fallacy of the undistributed middle term occurs.

At first, picturing in your mind the distribution statuses to determine the fallacy occurs will be challenging, but working through a few problems will presently become rewarding.

AAA-2

All P is M^U
All Sis M^U
All S is P

Since both premise predicate classes are undistributed, the fallacy of undistributed middle term occurs.
EAE-1

No M^D is P
All S is M^U
No S^D is P

The E major premise distributes all terms, so the undistributed middle falllacy does not occur.

(The EAE-1 syllogism is the second most common valid syllogism found in argumentation.)
AAI-2

All P is M^U
All S is M^U
Some S is P

Since both premise predicate classes are undistributed, the fallacy of undistributed middle term occurs.
AII-4

All P is M^U
Some M^U is P
Some S is P

The middle term is undistributed in both premises, so the fallacy of the undistributed middle occurs.
OAO-4

Some P is not M^U
All M^D is S
Some S is not P^D

The middle term is distributed in the minor premise so the fallacy of the undistributed middle does not occur.

(Later we will learn since the P term is undistributed in a premise but distributed in the conclusion, the fallacy of the illicit major term occurs since only some Ps are referred to in the premises but all Ps are referred to in the conclusion. Reasoning from “some” to “all” is not deductive reasoning.)
III-1

Some M^U is P
Some S is M^U
Some S is P

The middle term is undistributed in both premises, so the fallacy of the undistributed middle occurs.
AAA-1

All M^D is P
All S is M^U
All S is P

The middle term is undistributed in both premises, so the fallacy of the undistributed middle occurs.

The AAA-1 syllogism is the most common occurring valid syllogism used in deductive argumentation.
OII-3

Some M^U is not P
Some M^U is S
Some S is P

The middle term is undistributed in both premises, so the fallacy of the undistributed middle occurs.
OIO-2

Some P^U is not M^D
Some S is M^U
Some S is not P^D

The middle term is distributed in the major premise, so the fallacy of the undistributed term does not occur.

(Later we will study the fallacy of the illicit major term where the major term P is undistributed in a premise but distributed in the conclusion. Again, reasoning from “some” to “all” is not deductive reasoning.)
EOI-1

No M^D is P
Some S is not M^D
Some S is P

The middle term is distributed in both premises so the fallacy of the undistributed middle does not occur.

(Later we will learn that all syllogisms with two negative premises are invalid arguments.)

Adapted from “Der Schwermütige Ajax mit Termessa und Eurysakes,” A.J. Carstens watercolor, 1791, Kunstsammlungen zu Weimar

Evaluate the following two syllogisms stated by Biron, a lord attending the king, in Shakespeare's Love's Labor Lost:

“Well, ‘set thee down, sorrow!” for so they say the fool said, and so say I, and I the fool. Well proved, wit. By the Lord, this love is as mad as Ajax: it kills sheep; it kills me — I am sheep. Well proved again o’ my side.”[4]

Hint: the arguments can be setup as follows:

Argument 1:
The fool said “Well, set thee down sorrow!”
I said “Well, set thee down sorrow!”
∴ I am a fool.

Argument 2:
Sheep are killed by a love as mad as Ajax.
I am killed by a love as mad as Ajax.
∴ I am a sheep.

Translate the arguments into standard order and form and test for validity.

Argument 1:

A fool is a person who said “Well … sorrow!”^U
I am a person who said “Well, … sorrow!”^U
I am a fool.

Venn Diagram AAA-2

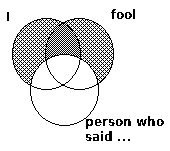The first argument commits the fallacy of the undistributed middle term.

Argument 2:

Sheep are mammals killed by a love as mad as Ajax.^U
I am a mammal killed by a love as mad as Ajax.^U
I am a sheep.

The second argument commits the fallacy of four terms since in the major premise “killed” denotes “caused to die” and in the minor premise denotes “caused pain.”

Notes

1. To say the revised argument is valid does not imply the revised argument is sound unless both of the premises presented are known to be true. This argument would be sound if all “social equality seekers” were understood to be narrowly classified as “feminists.”↩

2. John Buridan, Treatise on Consequences trans. Stephen Read (New York: Fordham University Press, 2015), 121. doi: 0.5422/fordham/9780823257188.001.0001 ↩

3. E.g., see Henry Joseph Turrell, A Manual of Logic, Or, A Statement and Explanation of the Laws of Formal Thought (London: Rivingtons, 1870), 105.)↩

4. Shakespeare, Love's Labor Lost IV iii.4. (In Homer's Illiad, Ajax lost his senses when he was not awarded Achilles’ armor by the Acheans, and thinking their sheep and cattle were Acheans, began killing the sheep and cattle.)↩

Syllogistic Fallacy 2: The Fallacy of the Undistributed Middle Term

Distribution:

Sound Argument

Notes

Syllogistic Fallacy 2:
The Fallacy of the Undistributed Middle Term