Return to Philosophy Web Homepagephilosophy.lander.edu

      Title: Introduction to Logic

Philosophy Homepage » Logic Homepage » Informal Fallacies » Nature of Logic

   

 

Quizzes
Tests
Links
Search
Readings
Syllabus

 

 

 _The Artes_of_Logike_and_Rethorike_

The Nature of Logic


Abstract: Logic is defined and described with examples; deductive arguments are distinguished from inductive arguments. Logic differs from psychology as it is a prescriptive science rather than a descriptive science.





  1. What is logic?

    Logic is the study of the methods and principles used in distinguishing correct from incorrect reasoning.


    1. As a discipline which evaluates arguments of different kinds, logic is the study of how a concluding statement logically follows from another statement or statements (termed premises) either with some probability or with certainty.


    2. Logic differs from psychology in being a normative or a prescriptive discipline rather than a descriptive discipline.


      1. I.e., logic prescribes how we ought to reason; it's not directly concerned with describing how people actually do reason in their everyday activities[1] — although both formal and informal logic are often used to evaluate reasoning in the public sphere.

      2. So, logic provides the rules for correct thinking, and identifies fallacies of incorrect thinking.

      3. Consequently, logic distinguishes good arguments from poor arguments.


    3. Important: The logic examples used in the remainder of this page are for illustration of the types of problems studied in this course. You are not expected to understand anything in detail — the examples are provided only to suggest some of the skills which will acquired in this course.


  2. How logic helps reasoning:


    1. The practice solving logic examples and constructing good arguments improves logic skills. Some examples of how this course can help our reasoning skill can be suggested by looking at a few common arguments.

      1. Consider the following syllogism from Thomas Blundeville's 1619 The Art of Logicke:

        “Every covetous man doth violate the Lawes of liberalitie;

        but every prodigall man doth violate the Lawes of liberalitie;

        therefore every prodigall man is a covetous man.”[2]


        In today's English, Blundeville is arguing here:
        Since both greedy people and wasteful people don't freely share, wasteful people are greedy.
        It will become easy for us to recognize the fallacy in this argument as a fallacy of the undistributed middle term. Or, in plain language, just because two different things are alike in one characteristic doesn't mean that one of them is necessarily part of the other.

        To glimpse why this is the case, consider that the argument is just like claiming:

        All dogs are animals.

        All cats are animals.

        ∴ All cats are dogs.

        The form of the Blundeville's argument and the form of the cat argument are identical.

      2. Evaluate the following informal argument stated by Air Chief Hugh Marshall Lord Dowding, who led the Royal Air Force in World War II:
        “More than 10,000 [UFO] sightings have been reported, the majority of which cannot be accounted for by any ‘scientific’ explanation … I am convinced that these objects do exist and they are not manufactured by any nation on earth. I can therefore see no alternative to accepting the theory that they come from an extraterrestrial source.[3]
        While this argument might seem convincing, consider this counter-example about money put under a child's pillow during the night after the child loses the first primary (baby) tooth[4]:
        In spite of the large number of quarters put under kid's pillows which can be attributed to sneaky parents, there are hundreds of cases which cannot account for the source of the money. Therefore, what better evidence could there be for the existence of the tooth fairy?
        The UFO argument is an example of an informal fallacy termed the argumentum ad ignoratiam; it's a common fallacy often used by promoters who have flimsy evidence to support their beliefs.


    2. As well, this course can help with “the negative approach” in that we can avoid errors by being aware of common mistakes in logic e.g., being aware of common formal and informal fallacies.


      1. For example, how would you evaluate the following argument drawn from dialogue in a novel:
        “Who did he think he was, Napoleon, because he was so short?”[5]
        In this short implicit argument, the fallacy of false cause (or non causa pro causa) occurs. If this inference were to be adequate, all, or most, short persons would have to presumed to become great like Napoleon.

      2. Here's another example of a common error from a historical study:

        “Contrary to the commonly held belief that in antiquity and as late as 1700 A.D. normal lifespan was about 35 years, there are indications that the ancient Greeks lived longer. … A limited number of skeletal findings and demographic data have encouraged amongst scientists and laymen alike the general opinion … the average length of life was about 35 years. …

        [But]

        All men living in Greece in the 5th and 4th century B.C. whose data of birth and death have been documented with certainty by grammarians and historians [were found to have a mean length of life of] 71 ± 13.4 years.”[6]

        The reasoning here is another kind of fallacy of distribution: there is an essential difference between an average lifespan estimate with infant mortality data included and an average lifetime estimate excluding that data.

        So the commonly held belief that the normal lifespan in antiquity was about 35 years confuses the “normal” lifespan with the average lifespan.


    3. Methods, criteria, and techniques, all are given in this course for the development of procedures to test for argument correctness. Here are some illustrations of a few approaches we will be learning and using in this course of study.


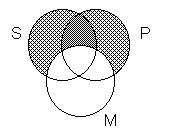
      1. For example, we can test problem I, A stated above by drawing a Venn Diagram to show the fallacy of the undistributed middle term. This can be facilitated by first “translating” the argument into a simplier form as follows:

    1. All [covetous men]P are [violators of liberality]M

      All [prodigal men]S are [violators of liberality]M

      Thus, all [prodigal men]S are [covetous men]P.

      1. Here, the shaded lines are drawn in those sections of the overlapping circles where the two premises indicate there is an absence of all individuals. Areas where no shaded lines are drawn are areas in which individuals have not been be eliminated by the two premises.

        So the first statement means that all of the P's (covetous men) are ”pushed into” the area of the M's (violators of liberality) — the empty lens area between the P and M circles.

        We can see there is a small area in the lower part of the S circle which is not shaded. The unmarked area indicates not all S (prodigal men) have been definitely excluded from the overlapping P (covetous men) circle.

        So the diagram indicates that the premises do not exclude the possibility that there could be some S's which are not P's. This means the premises do not prove with certainty that “All S's ([prodigal men) are P's (covetous men).

        So the conclusion of this argument has not been proved.[7]

      2. We can show the fallacy in this example by appealing to specific rules known rules of the syllogism by looking at its form:

        All P is M U

        All S is M U

        All S is P

        The term M shared by both premises is said to be undistributed because as part of the predicate of these two statements, M does not refer to each and every person who is a violator of liberality, but only those M's who are either covetous or prodigal men. But these are not the only persons who are violators of liberality. We cannot be sure that either the covetous or the prodigal men referred to in these statement have any definite relation specifically to each other.

        So the fallacy of the undistributed middle term is based on the violation of a rule like this:

        Rule: In a valid standard form categorical syllogism, the middle term must be distributed in at least one premise.
        Another way to envision this fallacy is to study the following diagram:

        Diagram of Undistributed Middle Term

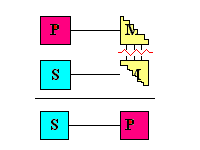
        For the two terms of the conclusion to be connected through the third, as in the mechanism shown here, at least one term must be related to the whole of the class designated by the middle term.


    1. There are many kinds of logic which exhibit a kind of family relation to each other: dialectic, classical, symbolic, multivalued, deontic, fuzzy, etc.


    2. In this course, basically, we will study two general types of logic: classical deductive and inductive logic.


      1. Deductive Logic is concerned with determining when an argument is valid (i.e., deals with conclusive inferences).


        1. A deductive argument is one in which it is claimed that the conclusion follows with necessity.


        2. If that claim is not met, then the argument is said to be invalid.

        3. Consider this example from Time magazine discussion about the assassination of U.S. President John F. Kennedy:
          “Since tests proved that it took at least 2.3 seconds to operate the bolt on Oswald's rifle, Oswald obviously could not have fired three times — hitting Kennedy twice and Conally once — in 5.6 seconds or less.“[8]
          The Time magazine essay assumes it takes 2.3 seconds to load a round and fire one shot, so it would would require 6.9 seconds to fire three shots:

          2.3 sec. — 1st shot.

          2.3 sec. — 2nd. shot.

          2.3 sec. — 3rd shot.

          6.9 sec. — total time.

          So under these assumptions the assassin Lee Harvey Oswald could not have fired all three shots. In a subsequent issue of Time, Frederick T. Wehr points out that this apparently indisputable argument was fallacious:
          “This argument, which has appeared in many publications since the assassination, is faulty, and I am surprised that I haven't seen it refuted before this. Assuming that the bolt of Oswald's rifle can, in fact, be operated in 2.3 seconds, then Oswald definitely could fire 3 shots in less than 5.6 seconds, for a stop watch would be started when the first shot was fired; the second shot would be fired when the stop watch read 2.3 seconds, and the third shot would be fired when the stop watch read 4.6 seconds. You have apparently overlooked the fact that, in the time it takes to fire 3 shots, it is only necessary to operate the bolt twice.”[9]
          The time for the first load need not be counted since Oswald could have loaded the cartridge well before the first shot was fired.

          0.0 sec. — 1st shot.

          2.3 sec. — 2nd. shot.

          2.3 sec. — 3rd shot.

          4.6 sec. — total time.

          Consequently, the rifle could have been fired in 5.6 seconds or less.


      2. Inductive Logic is concerned with the correctness of inferences for which the evidence is not conclusive — inductive logic involves only probable inferences.


        1. Hence, an inductive argument is one whose conclusion is claimed to follow with probability.

        2. Consider this example from Mark Twain:
          “[A]t bottom I did not believe I had touched that man. The law of probabilities decreed me guiltless of his blood, for in all my small experience with guns I had never hit anything I had tried to hit and I knew I had done my best to hit him.”[10]
          Within the context of the fictional story, Mark Twain's humorous retelling is an argument whose reasoning would result in a conclusion with some probability.[11]

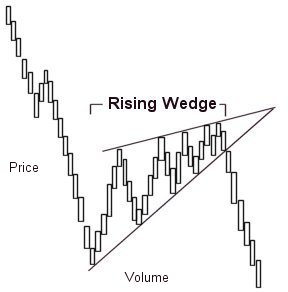        3. Plot of Falling Wedge Stock Market Trend. Source: Wikipedia, Atafqadir Or consider the inductive extrapolation techniques used in stock market prediction by Wall Street traders, e.g., the wedge formation in a stock chart:

          Stock market analysts argue that the rising-wedge trend signals a downward trend in a stock or bond price based on past experience. The inductive claim is that this trend will probably continue to be mostly reliable for future stock and bond price wedge-formations.


    3. What logic is not:


      1. Logic is not the science of the laws of thought; hence, logic is distinguished from psychology which is a descriptive science.[12]

        1. Sometimes people can come to realize future possibilities — conclusions reliably reached without being able to know or explain how the conclusion came about. E.g., C.J. Jung suggests that such an ability is characteristic of the intuitive type of personality.[13]

          The unconscious “logic” involved here is part of psychology, not logic.

        2. Often people can come to the right conclusion for the wrong reasons; however, logic is the study of the modes of correct reasoning which arrive at the right conclusion manifested in an prescriptive, not descriptive, manner.


      2. Logic is not really the science of reasoning either because the logician is not interested, as we have said, in the psychological processes of reasoning.

        1. Instead, logicians are interested in the structure of arguments.

        2. In sum, people infer statements and statements entail other statements.

        3. An entailment can hold between statements even though, at the time, it could be that no one understands the entailment is correct.

      Logic Homepage

      Notes: Nature of Logic

      Hyperlinks go to page cited.

      1. E.g. Immanuel Kant writes, “Logic does not really contain the rules in accordance with which man actually thinks but the rules for how man ought to think. For man often uses his understanding and thinks otherwise than he ought to think and use his understanding.” Immanuel Kant, The Bloomberg Logic in Lectures on Logic trans. J. Michael Young (Cambridge: Cambridge University Press, 1992), [26] 13.↩

      2. Thomas Blundeville, Arte of Logicke — Plainly Taught in the English Tongue (London: William Stansby, 1919), 184. Spelling wasn't standardized until the last part of the 18th century with Samuel Johnson's dictionary.↩

      3. Air Chief Marshall Lord Dowding quoted in Alfred L Webre, Exopolitics: Politics, Government and Law in the Universe (Vancouver, B.C.: Universebooks, 2005), 112.↩

      4. Folklore in many Western-influenced countries includes the notion that the Tooth Fairy (a mythical figure) will bring money during the night in exchange of the tooth.↩

      5. W. E. B. Griffin, The Lieutenants: Brotherhood of War I (New York: Penguin, 1982), 352. Actually, as many historians have pointed out, Napoleon Bonaparte was about average height of other men of his time.↩.

      6. Menelaos L. Batrinos, “Historical Note: The Length of Life and Eugeria in Classical Greece,” Hormones 7 no. 1 (January, 2008), 82-83. doi: 10.14310/horm.2002.1111041↩.

      7. Do not be concerned if you do not understand the diagram illustrated for this argument. At this point in the course, the example is provided only as an illustration. Later in the course, the interpretation of these diagrams will be more slowly and carefully explained.↩

      8. Editors, “Essay: Autopsy on the Warren Commission,” Time 88 no. 12 (September 16, 1966).↩

      9. Frederick T. Wehr, “Letters,” Time 88 no. 14 (September 30, 1966), 16. (accessed 2020.09.20)↩

      10. Mark Twain, “The Private History of a Campaign that Failed,” in The Complete Works of Mark Twain: The American Claimant Vol. IV, Authorized Edition (1872 New York: Harper and Brothers, 1924), 279.↩

      11. Historically, arguments in fictional writing have a controversial status since, strictly speaking they are false statements. In this course, we use fictional arguments to avoid traditional pedantic examples. So fictional arguments can be thought of in terms of a hypothetical supposition of truth in a thought-experiment. ↩

      12. The definition of logic as “science as the laws of thought, as thought” gained wide popularity following Sir William Hamilton's footnote in his edition of The Works of Thomas Reid [ed. Sir William Hamilton (Edinburgh: MacLachlan, Stewart, 1856), 698]. And in his Lectures on Metaphysics and Logic [eds. John Veitch and Henry L. Mansel (New York: Sheldon, 1858), I:87] Hamilton states:

      “Logic is the science of the laws of thought, in relation to the end which our cognitive faculties propose, — i.e. the true”

      Hamilton's definition was cited in William Spalding's entry “Logic” in the 1858 Encyclopæia Britannica and subsequently used in many prominent 19th century logic texts. This definition has occurred as late as 1914 in George H. McNair's A Class Room Logic, Deductive and Inductive (Nyacjm NY: Ethlas Press), 4.↩

      13. C.G. Jung, Psychological Types; or The Psychology of Individuation trans. H. Godwyn Baynes (New York: Harcourt, Brace, 1923), 461-466. See also this site “Jung's Psychological Types”↩

      Return to Logic Homepage
 
Philosophy and Logic  Top of Page  The Structure of Arguments

Send corrections or suggestions to larchie[at]philosophy.lander.edu
Read the disclaimer concerning this page.
1997-2021 Licensed under GFDL and Creative Commons 3.0



The “Copyleft” copyright assures the user the freedom to
use, copy, redistribute, and make modifications with the same
terms. Works for sale must link to a free copy.

The “Creative Commons” copyright assures the user the
freedom to copy, distribute, display, and modify on the same
terms. Works for sale must link to a free copy.

Arguments | Language | Fallacies  | Propositions  | Syllogisms  | Translation  | Symbolic

.