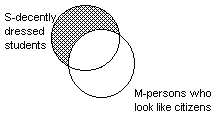Syllogistic Terminology

philosophy.lander.edu

Homepage > Logic > Categorical Syllogisms > Syllogistic Terminology > Part I

Quizzes

Tests

FAQ

Links

Search

Readings

Archives

Syllabus

*Philosophy 103: Introduction to Logic* *Syllogistic Terminology, Part I*

Abstract: Today's class introduces the logical terms used to describe two-premiss arguments composed of categorical statements. As a stalking horse, we analyze two arguments and test them for validity by means of Venn Diagrams.

The Notes to Syllogistic Terminology are in two parts:

Part I: Introduction of the Terms of the Syllogism
Part II: Review and Practice with Syllogistic Terminology

Part I: Introduction of the Terms of the Syllogism

Let us evaluate the following argument offered by Councilman William Meyers: "University students should have the right to graduate, if they dress decently. When you accept the responsibility of graduation into our society, you should look like a citizen."

As we analyze Councilman Meyers' argument, we will introduce the nomenclature of syllogistic arguments.

In order to evaluate this casual argument with charity, we need to be able to translate the argument reliably into standard-form categorical propositions.

The first step is to find the conclusion: "University students should have the right to graduate, if they dress decently."
1. The conclusion has the form: p if q, where p and q stand for different statements. Such conditional statements are often best handled with symbolic logic, but here we want to analyze the argument in terms of categorical form.
2. Let's step back and see what "p if q" means. Suppose p stands for "the bird is black" and q stands for "the bird is a raven." Our statement form, "p if q," in this case, would be, "The bird is black, if it is a raven." In standard categorical form, we could translate, "All ravens are black."
3. Using this model, we can translate Meyers' conclusion as "All decently dressed persons are persons with the right to graduate."
  1. The subject of the conclusion is called the minor term of the syllogism: "decently dressed students."
  2. The predicate of the conclusion is called the major term of the syllogism: "persons with the right to graduate."
The second step is to find the premisses and put the syllogism into standard order and form.
1. Standard form indicates that all the statements are standard-form categorical propositions (A, E, I, or O).
2. Standard order indicates that the statements are put in the sequence of the major premiss first, the minor premiss second, and the conclusion third. Thus, to find the standard order of a syllogism, we need to first find out what the major and minor premiss are.
  1. Not surprisingly, the major premiss is the premiss containing the major term. The major premiss is conventionally labeled with the letter 'P."
  2. Likewise, the minor premiss is the premiss containing the minor term. The minor term is labeled by convention with the letter "S."
3. Mr. Meyers gives only one premiss: "When you accept the responsibility of graduation, you should look like a citizen."
  1. The first part of the premiss, "When you accept the responsibility of graduation..." is meant to represent the same class as "persons with the right to graduate."
  2. Since "persons who have the right to graduate" is the predicate term of Mr. Meyers' conclusion, this premiss is our major premiss.
  3. We can now translate the premiss to read in categorical form: "All persons with the right to graduate are persons who look like citizens."
4. Mr. Meyers' argument can now be put as follows:
  
  All persons with the right to graduate are persons who look like citizens.
  
  ....{no minor premiss present yet}....
  ___________________________________
  All decently dressed people are persons with the right to graduate.
  1. Since, his premiss contains the major term, it is called the major premiss and is put first in the argument.
  2. Mr. Meyers is assuming his listeners will supply the missing premiss. When an argument is elliptical in this manner (i.e., with a missing statement), the argument is called an enthymematic argument.
  3. The missing premiss is the minor premiss and thus contains the minor term, "decently dressed students."
  4. So the only statement which makes sense as the minor premiss is the statement, "all decently dressed students are persons who look like citizens."�
    
    (By� the principle of charity, we suppose Mr. Meyers is assuming the most reasonable premiss.)
5. The term occurring in both premisses, but not in the conclusion is called the middle term and is symbolized by the letter "M."
6. The categorical syllogism can now be put as follows.

	P--MAJOR TERM		M--MIDDLE TERM
All	[persons with the right to graduate]	are	[persons who look like citizens].
	S--MINOR TERM		M--MIDDLE TERM
All	[decently dressed students]	are	[persons who look like citizens].

	S--MINOR TERM		P--MAJOR TERM
All	[decently dressed students]	are	[persons with the right to graduate].

The form of the syllogism can be conveniently put as

All P is M.
All S is M.
All S is P.
Two more terms are worth noting in our analysis of this syllogism. Logicians call the order of the names of the statements the mood of the syllogism. Mr. Meyers' syllogism is an AAA syllogism. Note that the mood does not uniquely describe the form of the syllogism, even though, by convention, the conclusion has the S and P term and the premisses contain the M term.
1. figure In other words, if all we knew about Mr. Meyers' syllogism was that it was an AAA syllogism, we can conceive of the following possibilities for the position of the middle term.

Figure 1	Figure 2	Figure 3	Figure 4
**M -- P	**P -- M	**M-- P	**P -- M
**S -- M	**S -- M	**M-- S	**M -- S
**S -- P	**S -- P	**S -- P	**S -- P

The position of the middle term is described by the figure of the syllogism. The figures are named "1," "2," "3," and "4." They are easily remembered because they form the shape of a flying brick.

Think of the M's being solid in the center with no other terms between them. Mr. Meyer's syllogism is an AAA-2 syllogism since the M term is in the predicate of both premisses.

The mood and figure uniquely describe the form of the syllogism. Any syllogism of this form will have the same degree of validity or invalidity. I.e., if Mr. Meyer's AAA-2 syllogism is invalid, then any other syllogism of the same form is invalid.

The third step is to test the syllogism by means of Venn Diagrams or the rules for validity. This might be a good time to review the symbols used to diagram the standard-form propositions.

The idea is to look at the logical geography of the premisses. If the argument is valid, the premisses should mark out the conclusion beyond doubt, without further markings.
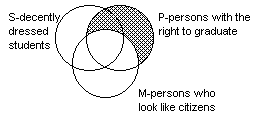
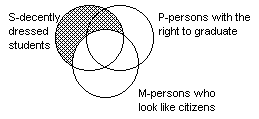
. The major premiss, "All P is M" would be diagrammed as the picture below. The diagram has been slanted so that it can be superimposed on the diagram for all three classes later.

The minor premiss, "All S is M" would be diagrammed as the picture below. It also has been slanted so it can be superimposed in the diagram above.

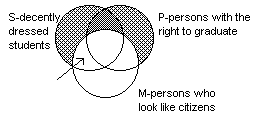
Putting both diagrams together on the representation of the S, P, and M classes would give a picture like the one below. Can we "read off" the conclusion without further markings? Is there any possibility of an S not being a P? Do diagramming the premisses without additional marking produce a diagram of the conclusion?
Since there is the possibility of an "S" being in the area marked, and it is outside of the P-area, the syllogism is invalid. Mr. William Meyer's syllogism is invalid.� He might have a false premiss as well.

Continue with Part II: Review and Practice with Syllogistic Terminology

Check your understanding with a Quiz on Syllogistic Terminology

Send corrections or suggestions to webmaster@philosophy.lander.edu
Read the disclaimer concerning this page.
11.24.04 � 2004 Licensed under GFDL