![]()
|
|
|
Homepage > Logic > Symbolic Logic > Conditionals
| Quizzes |
| Tests |
| FAQ |
| Links |
| Search |
| Readings |
| Archives |
| Syllabus |
 Philosophy 103: Introduction to Logic
Philosophy 103: Introduction to LogicConditional Statements and Material Implication
Abstract: The reasons for the conventions of material implication are outlined, and the resulting truth table for is vindicated.
- The word "implies" has several different meanings in English, and most of these
senses of the word can be conveyed in the ordinary language connection of statements
with "If … then …" In symbolic logic, implication is present for
"If … then …" propositions which assert some logical or causal or
other relationship.
- Implication is a relation that holds for conditional statements—there are
many types of conditionals:
- Logical: E. g., "If all philosophers are thinkers and John is
a philosopher, then John is a thinker."
- Definitional: E. g., "If Carol is anemic, then Carol has a low
concentration of erythrocytes in her blood."
- Causal: E. g., "If you strike the match, it will light."
- Decisional: E. g., "If you donate to educational
television, then the company you work for will match the amount."
- Logical: E. g., "If all philosophers are thinkers and John is
a philosopher, then John is a thinker."
- Material implication is the weakest common meaning for all types of "If …
then …" statements.
- By convention the first part of the conditional is termed the antecedent
(also less often called the "implicans" or the "protasis"), and the second part
of the conditional is the consequent (less often termed the "implicate" or
"apodosis").
E. g., in the conditional statement "If you study diligently, then you might see positive results," the antecedent is "You study diligently" and the consequent is "You might see positive results." - In general, the weakest common meaning is that (1)
if the antecedent and consequent
of a conditional statement are true, then the conditional as a whole is true, but (2)
if the
antecedent is true and the consequent is false, then the conditional as
a whole is
false.
- Thus, we can display these values in the following truth table:
p q p 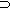 q
q
1 T T T 2 T F F 3 F T ? 4 F F ?
- By convention the first part of the conditional is termed the antecedent
(also less often called the "implicans" or the "protasis"), and the second part
of the conditional is the consequent (less often termed the "implicate" or
"apodosis").
- Implication is a relation that holds for conditional statements—there are
many types of conditionals:
- If we assume completeness for our truth functionality, then lines (3) and (4)
of the truth table for "p
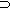 q"
must have truth values unique to the substitution instances for implication.
Let's try out various combinations of truth values.
q"
must have truth values unique to the substitution instances for implication.
Let's try out various combinations of truth values.
- If the resultant truth values for "p
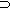 q"
on lines (3) and (4) of the truth table, were both false, then this
truth table would be the same truth table for conjunction (or the dot "
q"
on lines (3) and (4) of the truth table, were both false, then this
truth table would be the same truth table for conjunction (or the dot "  "). Consequently, these
two lines cannot both result in false because conditionals mean
something different from conjunctions.
"). Consequently, these
two lines cannot both result in false because conditionals mean
something different from conjunctions. - If the resultant truth values were a T and a F respectively, for lines (3) and (4)
of the truth table for "p
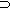 q", then the
truth of the conditional would depend on the truth of the consequent regardless of
the first statement.
q", then the
truth of the conditional would depend on the truth of the consequent regardless of
the first statement.
However, "If p then q" does not mean "q whether or not p." - If the resultant truth values were respectively a
F and a T for lines (3) and (4) of the truth table, then a similar objection would apply. This objection can be
explained with the help of the following tentative truth table:
p q p 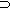 q
q
1 T T T 2 T F F 3 F T F? 4 F F T?
Suppose we have the conditional statement, "If the match is struck, the match lights." By the above truth table, if we do not strike the match and the match lights, then the conditional would be false. But surely the match could light in many other ways than the method of striking.
I. e., The tentative truth table implies the match lights only in case the match is struck; we want to allow that the match could light in other ways. - The final suggestion for the truth table for "
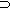 " for is this:
" for is this:
p q p 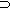 q
q
1 T T T 2 T F F 3 F T T 4 F F T
This interpretation we shall adopt even though it appears counterintuitive in some instances—as we shall see when we talk about the "paradoxes of material implication."
- If the resultant truth values for "p
- The conditional expressed by the truth table for " p
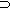 q " is called material
implication and may, for convenience, be called a fifth type of
conditional.
q " is called material
implication and may, for convenience, be called a fifth type of
conditional.
- So we have the following main kinds of conditionals: logical,
definitional, causal, decisional, and material.
- Note two points:
- The material kind of implication is not the only relation of
implication.
- Material implication does not somehow stand for all the
meanings of the "If … then … "
- The material kind of implication is not the only relation of
implication.
- But we can say that it has a common partial meaning with
all of the other kinds of conditional statements.
- So we have the following main kinds of conditionals: logical,
definitional, causal, decisional, and material.
- Another way of expressing the relation of material implication in in
terms of the dot symbol: ~ ( p
 ~ q ).
~ q ).
- That is, these expressions are equivalent:
[ ~ ( p ~ q ) ]
~ q ) ] 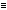 ( p
( p 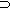 q )
q )
whatever the substitution instances for p and for q are, the truth values of each compound will remain the same. - Another way of expressing this relations, is to say that this
expression is a tautology—a statement form that has only
true substitution instances.
- We will express these ideas in terms of truth tables. But first, what is a truth table and how it is constructed is the subject of the next tutorial.
- That is, these expressions are equivalent:
Recommended Reading:
Level
Two Tutorials: Material Implication, an interesting discussion of the truth
table and interpretation of material implication.
Logical Conditional,
a brief authoritative summary of conditionals and related concepts.
A Comparison of Techniques for Introducing Material Implication,
a discussion of seven ways of introducing truth-functional definition of material implication
by Matthew C. Clarke at the University of Natal.
Send corrections or suggestions to webmaster@philosophy.lander.edu
Read the disclaimer
concerning this page.
06.27.05
© 2004 Licensed under GFDL
Arguments | Language | Fallacies | Propositions | Syllogisms | Translation | Symbolic
![]()
![]()
