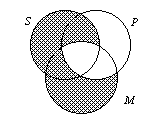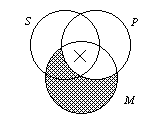Abstract: The
Venn Diagram technique is shown for typical as well as unusual syllogisms. The problem of
existential import is introduced by means of these diagrams.
I. One good method to test quickly syllogisms is the Venn Diagram technique. This class
assumes you are already familiar with diagramming categorical propositions. You might wish
to review these now: Venn Diagrams. |
|
A. A syllogism is a two premiss argument having
three terms, each of which is used twice in the argument. |
|
B. Each term ( major, minor, and middle terms)
can be represented by a circle. |
|
C. Since a syllogism is valid
if and only if the premisses entail the conclusion, diagramming the premisses will reveal
the logical geography of the conclusion in a valid syllogism. If the syllogism is invalid,
then diagramming the premisses is insufficient to show the conclusion must follow. |
|
D. Since we have three classes, we expect to have
three overlapping circles. |
|
|
|
 |
|
|
1. The area in the denoted circle
represents where members of the class would be, and the area outside the circle represents
all other individuals (the complementary class). The various area of the diagram are noted
above. |
|
|
2. Shading represents the knowledge that
no individual exists in that area. Empty space represents the fact that no
information is known about that area. |
|
|
3. An "X" represents "at least one
(individual)" and so corresponds with the word "some." |
| II. Some typical examples of syllogisms are shown
here by their mood and figure. |
|
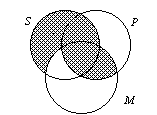
A. EAE-1 |
|
|
1. The syllogism has an E statement for
its major premiss, an A statement for its minor premiss, and an E statement
for its conclusion. By convention the conclusion is labeled with S (the minor term)
being the subject and P (the major term) being the predicate. The position of the
middle term is the "left-hand wing." |
|
|
2. The form written out is No M is P.
All S is M
No S is P. |
|
|
3. Note, in the diagram below, how the area in
common between S and P has been completely shaded out indicating that "No S is
P." The conclusion has been reached from diagramming only the two premisses.
All syllogisms of the form AEE-1 are valid. |
|
|
|
 |
|
B. AAA-1 |
|
|
1. This syllogism is composed entirely of "A"
statements with the M-terms arranged in the "left-hand wing" as well. |
|
|
2. Its form is written out as All M is P.
All S is M.
All S is P. |
|
|
3. Note, in the diagram below, how the only
unshaded area of S is in all three classes. The important thing to notice is that
this area of S is entirely within the P class. Hence, the AAA-1
syllogism is always valid. In ordinary language the AAA-1 and the EAE-1
syllogisms are by far the most frequently used. |
|
|
|
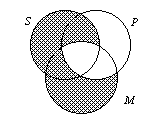 |
|
C. AII-3 |
|
|
1. The AII-3 syllogism has the M-terms
arranged in the subject position--the right side of the brick. |
|
|
2. This syllogism sets up as All M is P.
Some M is S.
Some S is P. |
|
|
3. When diagramming the syllogism, notice how you
are "forced" to put the "X" from the minor premiss in the area
of the diagram shared by all three classes. The "X" cannot go on the P-line
because the shading indicates this part of the SM area is empty. This "logical"
forcing enables you to read-off the conclusion, "Some S is P." |
|
|
4. This syllogism is a good example why the
universal premiss should be diagrammed before diagramming a particular premiss. If we
were to diagram the particular premiss first, the "X" would go on the
line. Then, we would have to move it when we diagram the universal premiss because the
universal premiss empties an area where the "X" could have been. |
|
|
|
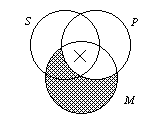 |
|
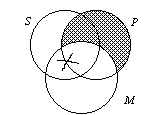
D. AII-2 |
|
|
1. The AII-2 has the M terms in the
predicate of both premisses. |
|
|
2. The syllogism is written out as All P
is M.
Some S is M.
Some S is P. |
|
|
3. The diagram below shows that the "X"
could be in the SMP area or in the SPM area. Since we do
not know exactly which area it is in, we put the "X" on the line, as
shown. When an "X" is on a line, we do not know with certainty exactly
where it is. So, when we go to read the conclusion, we do not know where it is. Since
the conclusion cannot be read with certainty, the AII-2 syllogism is invalid. |
|
|
|
 |
|
E. The final syllogism
described here, the EAO-4 raises some interesting problems. |
|
|
1. Notice that in this syllogism there are
universal premisses with a particular conclusion. |
|
|
2. Its form is written out as No P is M.
All S is M.
Some S is not P. |
|
|
3. And its diagram is rather easily drawn as |
|
|
|
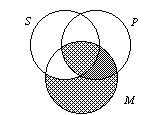 |
|
|
4. When we try to read the conclusion, we see
that there is no "X" in the SMP class. We must
conclude that the syllogism is invalid because we cannot read-off "Some S is
not P." |
|
|
5. However, if we know that M exists, all
the members of M have to be in the SMP class. These M's
are S's as well. Hence, we know that some S's are not P's! In other
words, the EOA-4 syllogism is valid if we know ahead of time the additional premiss
"M exists." |
|
|
6. Most contemporary logicians have concluded
that we should not assume any class exists unless we have evidence. |
|
|
|
a. We want to talk about theoretical entities without
assuming their existence. |
|
|
|
b. For example, in science and mathematics, our logic will
apply when talking about circles, points, frictionless planes, and freely falling bodies
even though these entities do not physically exist. |
|
|
|
c. This diagram illustrates the contemporary topic called the
problem of existential import. When can we reasonably conclude something exists? How
does this conclusion affect our theory of logical validity? |