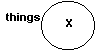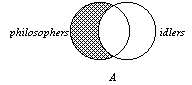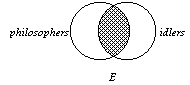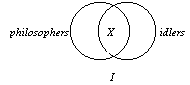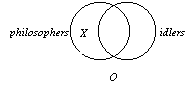Abstract: The
technique of representing statements by means of pictures is explained.
I. One way to view the "logical geography" of the standard-form categorical
propositions is to use diagrams invented by John Venn, a friend of Lewis Carroll. |
|
A. Perhaps, you have been
introduced to diagrams used in set theory; the Venn Diagrams are somewhat different. |
|
B. Most descriptions of Venn
Diagrams introduce the three symbols used as follows. |
|
|
1. An empty circle is used to
represent a subject class or a predicate class and is generally so labeled with an S
or a P. Putting the name of the actual subject or predicate class next to the
circle is preferred. The area inside the circle represents members of the class in
question, if there are any. The area outside the circle represents all other
individuals (the complementary class) if there are any. Note that the label
"things" is written outside the circle, even though "things," if there
are any, would be inside the circle. |
 |
|
|
2. Shading or many parallel
lines are used to indicate areas which are known to be empty. I.e., there are no
individuals existing in that area. E.g., the diagram to the right represents the
class of "Yeti." |
 |
|
|
3. The third symbol used is an "X"
which represents "at least one" or "some" individual exists in the
area in which it is placed. The diagram to the right indicates "some thing." |
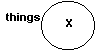 |
|
C. Perhaps the most important
symbol of all is the blank area where no marks of any kind are made. If an
area is not shaded or has no "X," then it is not considered empty,
but the blank area represents "no information is known." In other words, a blank
area represents the possibility of something existing in that area, nothing more. It is
also worth noting, that if an "X" is drawn on a line, the "X"
represents only the possibility of being "on either side," but where it is
exactly is not known. |
| II. Given this interpretation, the
four standard-form categorical propositions are diagrammed as follows. |
|
1. The A form, "All S
is P," is shown in the diagram to the right. Notice that all of the S's
are pushed out, so to speak, into the P class. If S's exist, they must be
inside the P circle since the left-hand lune of the diagram is shaded and so
is empty. |
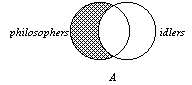 |
|
2. The E form, "No S
is P," is shown in the diagram to the right. Notice that the lens area
of the diagram is shaded and so no individual can exist in this area. The lens area is
where S and P are in common; hence, "No S is P." All
S, if there are any, are in the left-hand lune, and all P, if there are any,
are relegated to the right-hand lune. |
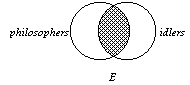 |
|
3. The I form, "Some S
is P," is much more easily seen. The "X" in the lens, as
shown in the diagram to the right, indicates at least one individual in the S class
is also in the P class. Note that the blank lunes indicate that we do not know
whether or not there are individuals in these areas. In fact, we have no information. |
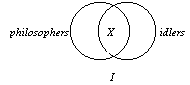 |
|
4. The O form, "Some S
is not P," is also easily drawn. The S that is not a P is marked
with an "X" in the S-lune. This area is not within the P
circle and so is not a P. It is worth while to note, that from this diagram we
cannot conclude that "Some S is P" because there is no "X"
in the lens area. Thus, studying this diagram will explain why "Some S is not P"
does not entail "Some S is P." |
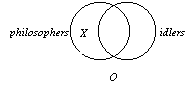 |
| III. For practice, diagram the
following statements. The diagrams provided in the answers are only partially correct
since they are generic A, E, I, or O diagrams. Your answers
should have the subject and predicate classes clearly labeled. |
|
1. All orchids are Cattyleas.
|
|
2. All ribosomes are structures in
the cytoplasm.
|
|
3. No Zurich gnomes are peddlers.
|
|
4. No rap is hard rock.
|
|
5. Some musicians are not
pianists.
|
|
6. Some dragsters are not funny
cars.
|
|
7. Some Presidents are forgetful
persons.
|
|
8. Some sculptors are not
painters.
|
| V. The use of Venn Diagrams to
evaluate two-premiss arguments is explained in the class concerning Syllogistic Venn Diagrams. |