![]()
|
|
|
Homepage > Logic > Categorical Syllogisms > Venn Diagrams
| Quizzes |
| Tests |
| FAQ |
| Links |
| Search |
| Readings |
| Archives |
| Syllabus |
Introduction to Logic
|
|
|
Abstract: The Venn Diagram technique is shown for
typical as well as unusual syllogisms. The problem of existential
import is introduced by means of these diagrams.
I. One good method to test syllogisms rapidly is the Venn Diagram technique. This class assumes you are already familiar with diagramming categorical propositions. If not, you might wish to review how to diagram standard form statements here: Venn Diagrams. |
||||
| A. The syllogism is a two premiss
argument having three terms, each of which is used twice in the
argument. |
||||
| B. Each term (major, minor, and middle
terms) can be represented by drawing a circle. Anything inside the
circle is designated as a member of the class named by that term and
anything outside the circle is something else. |
||||
|
C. Since a syllogism is valid if and only if the premisses
entail the conclusion, diagramming the premisses will exhibit the
logical geography of the conclusion. If the syllogism is invalid, diagramming the premisses will not show that conclusion necessarily follows from the premises. |
||||
D. Since we have three classes, we expect to have three overlapping circles. A diagram similar to this one was first used by John Venn [Symbolic Logic (London: Macmillan, 1818), 105]: |
||||
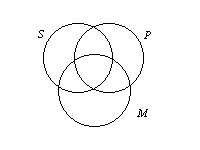 |
||||
| 1. The area within the denoted circle
represents where members of the class would be, and the area outside
the circle represents all other individuals (the complementary class).
The various areas of the diagram are noted above. | ||||
 2. Shading represents the knowledge no individual
exists in the class; for example, this diagram shows no
“Yeti” exists within the circle.
2. Shading represents the knowledge no individual
exists in the class; for example, this diagram shows no
“Yeti” exists within the circle.  Empty space represents the fact that no information is known whether
any thing exists in that area of the class.
Empty space represents the fact that no information is known whether
any thing exists in that area of the class. |
||||
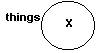 3. An “X” in the circle represents “at least one “thing”
” exists in the class of things, and so “X” here corresponds
with the word “some.”
3. An “X” in the circle represents “at least one “thing”
” exists in the class of things, and so “X” here corresponds
with the word “some.” |
||||
| II. Some typical examples of syllogisms are shown
here by their mood and figure. |
||||
| A. EAE-1 | ||||
| 1. The syllogism has an E statement for
its major premiss, an A statement for its minor premiss, and an
E statement for its conclusion. By convention the conclusion is labeled
with S (the minor term) being the subject and P (the major term)
being the predicate. The position of the middle term is the “left-hand wing” in this illustration of the syllogistic figures: 
|
||||
2. The form of this syllogism written out is No M is P. |
||||
| 3. We diagram one premiss at a time on the diagram of
three interlocking circles. So, as shown on the diagram below, we superimpose
the major premiss E statement diagram “No M is P”
on the area represented by the interlocking circles P and M. Next, we superimpose the A minor premiss “All S is M” on the interlocking circles S and M. Note, in the diagram below, how the area in common between S and P (called “the lens of the S and P classes) has been completely shaded out indicating that “No S is P.” No individual X can exist within the SP lens area because our diagram shows that area must be empty. In a sense, the conclusion “automatically” results from diagramming only the two premisses. We do not pencil in the conclusion — we merely read it out by observing the result of sketching the two premises. |
||||
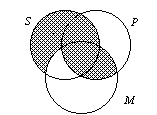
This diagram illustrates that all syllogisms of the form EAE-1 are valid because the diagram shows that if there are any Ss then they are in a completely separate area than Ps. |
||||
| B. AAA-1 | ||||
| 1. This syllogism is composed entirely of “A” statements with the M-terms arranged in the “left-hand wing” as was the syllogism above. | ||||
2. Its form is written out as All M is P. |
||||
| 3. Note, after diagramming the figure below, how
the only unshaded area of S is within the area of all three classes. The
important thing to notice is that this area of S is entirely within
the P class. Hence, we can conclude that if there are any Ss they have to be also in the P class. |
||||
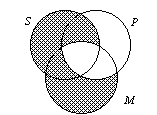
This diagrams shows all AAA-1 syllogisms are always valid. In ordinary language the AAA-1 and the (above) EAE-1 syllogisms are by far the most frequently used everyday syllogistic argument forms. |
||||
| C. AII-3 | ||||
| 1. The AII-3 syllogism has the M-terms arranged in the subject position — the right side of the orange flying brick diagram illustration above. | ||||
2. This syllogism sets up as All M is P. |
||||
| 3. When diagramming the minor premise of
this syllogism, notice how you are “forced” to put the
X from the minor premiss in the area of the diagram shared by all
three classes. The “X” cannot go on the P-line because the shading indicates that part of the SM lens area is empty. This “logical” forcing enables you to read-off the conclusion, that “Some S is P” because the X is in the union of S, P and M. |
||||
4. This syllogism is a good example why …
The universal premiss should be diagrammed before a particular premiss is diagrammed.If we were to diagram the particular premiss first, the “X” would go on the line. Then, we would have to move it when we diagram the universal premiss because the universal premiss empties an area where the “X” could have been. |
||||
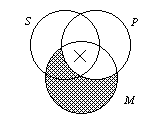 |
||||
| D. AII-2 | ||||
| 1. The AII-2 has the M terms in the predicate of both premisses. | ||||
2. The syllogism is written out as …All P is M. |
||||
| 3. The diagram below shows that the
“X” could be in the SM When an X is on a line, we do not know with certainty exactly where it is. So, when we go to read the conclusion, we do not know for sure whether the X is in the P class or not. Since the conclusion cannot be read with certainty, the AII-2 syllogism is judged invalid. |
||||
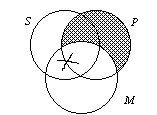 |
||||
| E. The final syllogism described here, the EAO-4 raises some interesting problems. | ||||
| 1. Notice that in this syllogism there are universal premisses with a particular conclusion. | ||||
2. Its form is expanded as …
No P is M. |
||||
| 3. And its diagram is rather easily drawn as … | ||||
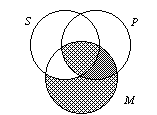 |
||||
| 4. When we try to read the conclusion, we see
that there is no “X” in the SM |
||||
| 5. However, if we independently knew that at least one
individual in the the class represented by M exists, then that one M
would have to be in the SM In other words, the EOA-4 syllogism is valid if we knew ahead of time the additional premiss “M exists.” |
||||
| 6. Most contemporary logicians have concluded that we should not assume any class exists unless we have some form of independent evidence. | ||||
| a. However, we often want to speculate about theoretical entities without assuming their existence. | ||||
| b. For example, in science and mathematics, our logic will apply when talking about circles, points, frictionless planes, and freely falling bodies even though these entities do not physically exist. | ||||
| c. This diagram illustrates the contemporary topic called the
problem of existential import. When can we reasonably conclude something exists? How
does this conclusion affect our theory of logical validity? |
||||
Check your understanding of
Venn Diagrams with a Quiz on Testing
Syllogisms
Readings: Venn Diagrams
A Survey of Venn Diagrams is a fascinating extension of the combinatorial properties of the diagrams by Frank Ruskey and Mark Weston, Department of Computer Science at the University of Victoria.Readings: Existential Fallacy
Bertrand Russell; Hugh MacColl, “The Existential Import of Propositions,” Mind New Series 14 no. 55 (July, 1905), 392-402. DOI: 10.1093/mind/xiv.3.398"“Does This Syllogism by Russell Show That Aristotelian Logic Doesn't Work,” Philosophy Stack Exchange: A discussion about Bertrand Russell's example criticism of Aristotle's syllogisms with this argument:
“If I were to say: ‘All golden mountains are mountains, all golden mountains are golden, therefore some mountains are golden,” my conclusion would be false, though in some sense my premisses would be true.”Gyula Klima, “Existential Import and the Square of Opposition,” in John Buridan (Oxford: Oxford University Press, 2009), 143-157. DOI: 10.1093/acprof:oso/9780195176223.003.0006
Bertrand Russell, “Aristotle's Logic,” in A History of Western Philosophy (1946 London: Taylor and Francis, 2005), 190.
Terence Parsons, “The Traditional Square of Opposition,” The Stanford Encyclopedia of Philosophy (Summer, 2017).
Abraham Wolf, The Existential Import of Categorical Predication (Cambridge University Press, 1905).
Michael Wreen, “Existential Import,” Crítica: Revista Hispanoamericana de Filosofía 16 no. 47 (August, 1984), 59-64.
Joseph S. Wu, The Problem of Existential Import (From George Boole to P.F. Strawson) Notre Dame Journal of Formal Logic X no. 4 (October 1969), 415-424. DOI: 10.1305/ndjfl/1093893792
Send corrections or suggestions to
larchie[at]philosophy.lander.edu
Read the disclaimer
concerning this page.
Last Updated 10-22-2018
1997-2017 Licensed
under GFDL

The “Copyleft” copyright assures the user the
freedom to use, study, redistribute, and make modifications
so long as that derivative works have the same or identical
license.
Arguments | Language | Fallacies | Propositions | Syllogisms | Translation | Symbolic
![]()
![]()