philosophy.lander.edu

Homepage > Logic > Syllogistic Terminology > Part II        

Part II: Review and Practice with Syllogistic Terminology

1. Let us review the foregoing terms and the procedures by evaluating another argument in summary fashion.
   
   
   1. While Mary Chaney was changing a flat tire, the car rolled forward off the jack bending the axle. The estimate to fix the car was $1,580. Mary's car was insured, so she filed a claim. The insurance adjuster said the claim could not be paid because the vehicle only had three wheels at the time of the accident and so was not an "auto." An "auto" is defined in the insurance policy as "a land motor vehicle with at least four wheels designed for use on public roads." Is the claim adjuster's argument valid?
      
      
   2. We will follows the rules of thumb described above to analyze the argument.
      
      
      1. First, find the conclusion. The adjuster concludes, "Miss Chaney's vehicle is not an insured auto." This is a singular statement and is, in effect, an E statement because it is universal negative with the subject and predicate undistributed. Usually singular statements are left as such rather than awkwardly translating into something like the following:

         "No things which are Miss Chaney's vehicle are insured autos." We will follow the former practice here.
         
         

      2. Second, put the syllogism into standard order and form.
         
         
         1. The reasons given for the conclusion are the statements taken from the insurance adjuster's claims that an automobile  must have at least four wheels and Miss Chaney's didn't.
            
            
         2. The first premiss, the major premiss, has to have the predicate term of the conclusion. It would be "All insured autos are land vehicles with at least four wheels.
            
            
         3. The second premiss, the minor premiss, has the subject term of the conclusion. It would be "Miss Chaney's vehicle is not a land vehicle with at least four wheels.  In sum, we have the following syllogism:
            
            

	P--MAJOR TERM			M--MIDDLE TERM
All	[insured autos]	are	[land vehicles with at least four wheels.]
	S--MINOR TERM			M--MIDDLE TERM
	[Miss Chaney's vehicle]	is not		[a land vehicle with at least four wheels.]
	S--MINOR TERM			P--MAJOR TERM
	[Miss Chaney's vehicle]	is not	[an insured auto.]

4. A moment's reflection gives us the following summary of the major parts of the argument and the common terms used to describe our two-premiss argument. (When analyzing syllogisms, one usually identifies the terms in the order sequenced here.)
   
   Categorical syllogism: The argument contains two premisses and a conclusion, and the argument contains three terms, each of which is used twice in the argument.
   
   Conclusion: "Miss Chaney's vehicle is not an insured auto.
   
   Major term: "insured autos.
   
   Minor term: "Miss Chaney's vehicle.
   
   Middle term: "land vehicles with at least four wheels.
   
   Major premiss: All insured autos are land vehicles with at least four wheels.
   
   Minor premiss: Miss Chaney's vehicle is not a land vehicle with at least four wheels.
   
   Mood: AEE 
   Figure: 2 
   Form: AEE-2
   
   
3. Test the syllogism for validity. The Venn Diagram representation of the insurance adjuster's argument could be presented in the following manner. The form of the syllogism is

   All P is M.
   No S is M.
   No S is P.
   

The major premiss, "All P is M," by itself can be diagrammed, as before separately.

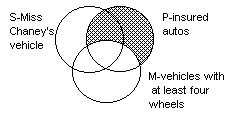The minor premiss, "No S is M," by itself can be diagrammed, separate from the whole, as well.

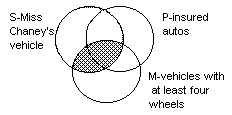Putting both diagrams together, if the syllogism is valid, we ought to be able to read off the conclusion, No S is P." Especially note that we do not diagram the conclusion.

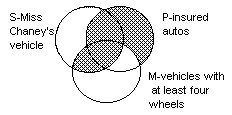4. Since the lens area in common between the S and P classes is completely shaded, we can read off the conclusion from the completed diagram. The insurance adjuster gave a valid argument. It is now up to Miss Chaney to question its soundness if she wishes to pursue her claim. Is there a false premiss in the argument? If so, even though the argument is valid, the argument does not prove the conclusion true.

For further practice, try the Quiz on Syllogistic Terminology.

Send corrections or suggestions to webmaster@philosophy.lander.edu
Read the disclaimer concerning this page.
       © 2004 Licensed under GFDL

Arguments | Language | Fallacies  | Propositions  | Syllogisms  | Translation  | Symbolic