Homepage » Logic » Argument Topics » Structure of Arguments

The Structure of Arguments

1. Background: Philosophy, Epistemology, and Logic

   1. We have seen that one main constituent of philosophy inquiry is epistemology, and one main aspect of epistemology is logic.

      
      

   2. Initially, the study of philosophy was broadly interpreted to be the systematic inquiry into the principles and presuppositions of any field of inquiry.

      
      

      1. Epistemology, as the theory of knowledge, is often briefly defined as the study of the nature, scope, limits of knowledge and justified belief.

         Logic was somewhat narrowly defined as the study of methods and principles used in distinguishing correct from incorrect reasoning.

         Formal logic emphasizes the study of the structure of arguments rather than their informational content.

         Informal logic is the investigation of ordinary language arguments. Reasoning in everyday life is emphasized through examination of rhetoric, fallacies, contextual relevancy, and effectiveness of reasoning.

         Logic provides a basis for evaluating claims of justification and knowledge but is not the be all and end all of a means by which to evaluate either philosophy, epistemology, or, for that matter, reasoning in other disciplines.

         
         

   3. Logic, as the study of correct reasoning, is used in every field of knowledge to assess reasoning as to the manner in which a field's established conclusions relate to its methods and particular assumptions. Additionally, understanding the logical connections within the subject matter requires an understanding of how issues in both semantics (language meaning) and syntactics (language structure, grammar) frame the relational logical structures of the field.

      
      

2. What is an Argument?

   1. The chief concern of (formal) logic is with the structures of arguments.

      
      

   Argument: any group of propositions of which one is claimed to follow logically from the others.

   
   

   1. In logic, the everyday sense of “argument,” such as my neighbor yelling to me about the noise I make with my trashcans, is not considered an “argument” in logic. Differences of opinion, emotional accusations, and verbal controversies are seen from a logical point of view as different varieties of disagreement. (These kinds of disputes are studied later in the course.)

   2. Our definition of “argument” is more of a theoretical definition than it is a lexical (i.e., dictionary) definition.

      An “argument” in logic is “a demonstration, justification, proof, or, in some cases, the explanation of some other statement (the conclusion)” — not that of an emotional quarrel or altercation.

   3. Sometimes an argument as a proof probably demonstrates its conclusion (as in an inductive argument); sometimes the proof is claimed to absolutely prove its conclusion (as in a deductive argument).

      1. If an argument is claimed to absolutely prove its conclusion and does not do so, the argument is faulty. For example, in the following argument …

         That bird is a fish crow; therefore, it's black.

         … the argument might be thought to be deductive as determined by the lexical meaning of the word “crow.” However, we must allow that the argument is, strictly speaking, a highly probable inductive argument due the extremely rare existence of albinism in crows.

      2. Often, in order to clearly evaluate the logical aspects of a disagreement, frequently we need to tease out the emotional and verbal aspects of the dispute in order to isolate and then evaluate its informational content in order to see if there is a logical disagreement present.

   4. Personal opinions are never arguments per se unless reasons are given in logical support of those opinions. Thus, the conclusion of an argument is not just someone's opinion to be freely accepted or rejected regardless of cogency of the premises, unless, of course, the reasons adduced for that conclusion are faulty.

      When persons differ in opinion, that difference is usually best settled by whomever can provide the more reasonable statements in logical support of their point of view.

      
      

   2. The essential parts of an argument are:

      1. Premise: a statement or proposition which gives reasons, grounds, or evidence for accepting some other statement or proposition, termed the conclusion.

      2. Conclusion: the statement or proposition, which is claimed to be established on the basis of other statements or propositions called premises.

         
         

3. An Example of a Typical Argument Showing the Difference Between an Inference and an Entailment

   1. Gestalt psychotherapist Fritz Perls once suggested the following argument:

      If we set our ideals too High, then we will Not meet those ideals.

      If we do Not meet those ideals, then we are Less than we could be.

      If we are Less than we could be, then we Feel inferior.

      ∴ If we set ideals too High, then we Feel inferior.[1]

      
      

      1. By convention, the reasons or premises are placed above a line that separates the premises from the conclusion. The three-dot symbol represents the function of a word like “therefore” or “hence” in ordinary language.

      2. As you read the passage and come to understand the argument, this experience is a psychological process called “making an inference.”

         
         

         An inference is the reasoning process by which a logical relation is understood.

         
         

         1. The logical relation is considered to be either valid (good) or invalid (not good), independently of whether or not we understand the inference (i.e. understand the reasoning). In other words, it is convenient to consider the logical relation as not being dependent for its validity on the psychological process of trying to understand why the conclusion logically follows from the premises.

            Validity is not determined by what we think; validity is determined by the rules of formal logic.

         2. It's not quite correct to define logic as “the science of reasoning” if this definition suggests that logic is a descriptive science like physics, chemistry, or some other empirical science. Instead, logic is a prescriptive science (like mathematics) because logic prescribes how one ought to reason rather than how one actually does reason.

            
            

   2. The prescriptive logical relation between the premises and conclusion in Perl's argument sketched above is claimed to hold regardless of whether or not we understand why the conclusion logically follows with certainty from the premises.

      
      

      1. In Perls' argument in the text-box above, we can symbolize the statements by using the bold letters in the text in order to see the structure of the argument, as follows:

         H → N

         N → L

         L → I

         H → I

         This kind of formal logical relation between premises and conclusion where the conclusion follows necessarily from the premises is termed an entailment.

         
         

         An entailment is a logical relation between or among propositions such that the truth of one proposition is determined by the truth of another proposition or other propositions, and this determination is a function solely of the meaning and syntax of the propositions concerned.

         
         

      2. Another way to remember the difference between an inference and an entailment is to note that people infer a conclusion, and propositions entail a conclusion.

      3. An understanding of argument structure is the sum and substance of formal logic. In informal logic meaning, justification, context-dependence, and fallacy theory are emphasized.[2]

      4. By the way, note that Perls' argument has a good (valid) structure, so if the conclusion is false, one of his assumptions (i.e. one of his premises) has to be false. The reason is that in a valid (good) deductive argument (an argument claiming the conclusion follows with necessity), if the premises are true, then the conclusion also necessarily follows as true also.

         1. If you have the intuition that something seems dubious about this argument, you are correct.

         2. The error in Perl's argument is not a formal error. The mistake made is in the premises. In the first premise Perl states that we cannot meet goals that are too high, so his second premise is inconsistent with that assertion. Namely, we are not be less than we could be if we failed to meet goals that not possible to meet. Perls equivocates on the use of the notion of “too high ideals.”

         3. Consequently, the ambiguous premises do not entail the conclusion.

            
            

4. What is the Difference Between a Statement and a Sentence?

   1. We have defined an argument in terms of a relationship between propositions or statements. In this course, statements are not distinguished from propositions. The terms are used interchangeably (even though, historically, some logicians have offered differing precising definitions of these terms).[3]

      
      

   2. In deductive or formal logic, a statement or proposition can be generally thought of as follows:

      
      

      A statement or a proposition is a sentence which has a truth value (i.e. is true or false but not both) even though that truth value might not be known.

      
      

      1. A statement is often thought of as occurring as a historical event: a linguistic expression with reference to some state of affairs at a particular time. In general, it is safe to say that a statement is true when it is factual or ultimately refers to something that is the case. In other words, a state of affairs (whether stated in words or not) determines whether or not a statement or proposition is true.[4]

      2. Some statements, however, are considered true universal statements — these statements are either considered true by definition or true as some sort of empirical generalization.

         (Sometimes, of course, definitions, empirical laws, or accidental generalizations are revised or improved as inaccuracies are discovered — e.g., when Einstein found Newton's law of gravity to be a useful approximation but unable to explain certain kinds of phenomena or when Willem de Vlamingh discovered black swans in Western Australia in 1697 disproving the belief that the existence of black swans was impossible.)

      3. On occasion, we do know the truth value of a proposition — especially in cases of vague, rhetorical, ambiguous, or empirically uncertain statements. The veracity of many statements depend on how they are interpreted, the context in which they occur, and their intended purpose.[5]

      4. Note that a sentence is considered to be a statement even if the truth-value of the statement is not known so long as it is known that the sentence has a truth value.

         For example, the sentence “Tomorrow it will rain,” when uttered or written on a particular occasion, is a proposition or statement, even though its truth or falsity can only be determined tomorrow.

      5. Most logic textbooks currently gloss over some of the practical problems with thoroughly understanding the nature of statements by treating all arguments as being composed of exclusively true or false declarative sentences. For the most part, this straightforward approach is also taken in these notes.

         But not all statements are declarative sentences. For example, if a taxi passenger were to ask the driver …

         “Do you really think it's a good idea to drive this fast?”

         … the passenger is most likely not asking for the taxi driver's opinion, but instead the passenger is stating the taxi driver is driving too fast.

      6. When we turn to evaluate arguments in everyday use, proper interpretation of what is said often requires great skill of translation into logical form. For example, almost seventy-five years ago, ordinary language philosopher J.L. Austin wrote:

         “We say, for example, that a certain statement is exaggerated or vague or bald, a description somewhat rough or misleading or not very good, an account rather general or too concise. In cases like these it is pointless to insist on deciding in simple terms whether the statement is ‘true or false.’ Is it true or false that Belfast is north of London? That the galaxy is the shape of a fried egg? … There are various degrees and dimensions of success in making statements: the statements fit the facts always more or less loosely, in different ways on different occasions for different intents and purposes.”[6]

         When sentences such as these occur, especially in literature, ethics, or religion, logicians do not always agree on how to interpret them. An intended argument composed of sentences with no conventionally explicable meaning fails to be an argument since the statements cannot faithfully be attributed a truth value.

         When such statements as Austin mentions occur in arguments in need of evaluation, the statements must be translated from ordinary language into emotively neutral and more precise wording along with any necessarily contextually assumed statements — all resultant statements based on the context of the circumstances in which they appear in accordance with the principle of charity.

         If the situation is one where truth is sought, the use of the principle of charity is essentially a best attempt at a fair and impartial rephrasing of the argument before evaluation. If the situation is one where persuasion is sought, as in a debate or in defense of a policy, then the strict principle of charity need not be followed. However, an interpretation of an opposing view in debate or a disputation seeking consensus ought not be distorted, else a straw man fallacy occurs.

         Later in this course we will study some statements appearing in arguments which are not framed in declarative sentences. In everyday discourse, statements can be expressed in any sentence type whether interrogative, exclamatory, or imperative, depending on the context in which the sentence occurs.

      7. It might be worth while to consider a particular example to illustrate how sentences which first appear not to be meaningful statements can occur in a context whereby they actually do so.

         

         At first glance that the vagueness of the isolated sentence “Ripeness is all” does not seem to have a truth value. However, consider the following passage in which this sentence occurs in Shakespeare's play King Lear when Gloucester while retreating from battle, blind and despondent, tells his disguised son he cannot go any farther. Edgar replies:

         Edg. Give me thy hand, come on.

         Glo. No further, sir; a man may rot even here.

         Edg. What, in ill thoughts again? Men must endure

         Their going hence, even as their coming hither:

         Ripeness is all: come on.

         [Lear V.II.5-11 (B. Kellogg, 1886)]

         Edgar is apparently speaking of the significance of this moment in life, itself, as a point in Glooucester's lifespan whereby he, as any person must, continue to persist courageously until the inevitable end. He assures Gloucester that the pivotal time has “ripened” to the moment he must now act. “Ripeness is all” in this context is translatable as a proposition something like, “Always take advantage of the fullness of an opportunity to act at the appropriate time.”

         This example was chosen to illustrate another complicating aspect of the nature of statements. Namely, in general, the truth value of statements in fiction is not to be considered true in the sense of corresponding to an actual state of affairs in the world. One way fictional statements can be seen to have truth value is to view fictional statements as being true relative to the imaginative state of affairs described in the work. “Ripeness is all” as said in King Lear and interpreted here, can be understood both as a literary truth and, as well, a moral truth in the everyday world.

         
         

   3. Most of logic is solely concerned with statements having truth values, so you can see that much of what is said during the ordinary course of our lives is not argumentative in the logical sense and is not to be understood in terms of being true or false.

      Consider, for the moment, the confusion that could result if we were to deem the following sentences to be statements.

      1. At breakfast, your friend sleepily mumbles,

         “Good Morning.”

         [We'd miss the point by responding “What's so good about it?”]

      2. In the work breakroom, your co-worker greets you with,

         “You've looking good today.”

         [It would be inappropriate to reply, “Well, you're wrong — I just saw my doctor yesterday and …” Greetings aren't usually intended to have truth values.]

      3. A poet writes,

         “And what is so rare as a day in June?
         Then, if ever, come perfect days; …”[7]

         [To respond “Well, I don't think so; the month of May has some pretty fine days,” would be an inappropriate response to a expressive passage written to extol the beauty in nature at that time of year.]

      4. A guest at a coffee shop says to a waitress:

         “I'd like a cup of coffee.”

         [The waitress would miss the point of the directive use of language by interpreting the statement as informative (i.e. true or false) if she were to answer, “Yeah, speaking of things you'd like, I bet you'd like to have a BMW more.”]

      5. Thus, phatic communication,
         close ×

         phatic communication:

         “[W]e have here a new type of linguistic use — phatic communion … a type of speech in which ties of union are created by a mere exchange of words. … Are words in Phatic Communion used primarily to convey meaning[?] … Certainly not! … Each utterance is an act serving the direct aim of binding hearer to speaker by a tie of some social sentiment or other.
         
         [Bronisław Malinowski, “The Problem of Meaning in Primitive Language” in C.K.Ogden and I.A. Richards, The Meaning of Meaning 2nd ed. (New York: Harcourt Brace, 1927), 315.
         greetings, commands, requests, and poetry, among other uses of language, are not meant to be taken as statements under normal conditions.
         

   4. In sum, there are different ways in which all statements or propositions, regardless of their degrees of success, are sentences, but not all sentences are statements because some sentences are not intended to have truth values.

   
   

5. Self-Test: Which of these Sentences are Statements?

   Many of the following exercises are challenging on account of (1) no background circumstances are provided to frame a context and (2) historically, logicians would differ on some of the interpretative suggested answers provided..

   Carefully read each of the following sentences and state whether or not each sentence is likely to be used as a statement in ordinary everyday circumstances. If the sentence is evaluated as not a statement in most circumstances, can you envision circumstances whereby the sentence would function as a statement in that context?

   ---

   
   
   Show All Answers   Hide All Answers   Print with Answers
   
   
   

   1. The core of the dwarf planet Pluto is iron ore.

      Answer
      

      Since iron ore either is, or is not, the core of Pluto, the sentence is either true or false. Thus, it is a statement. An inductive argument as to the possibility of Pluto having iron ore would that since most solar system planets have iron-rich cores, probably Pluto does also.

   2. Tomorrow it will rain.

      Answer
      

      Since either rain will or will not fall tomorrow, the sentence has a truth value, so it's a statement. If someone were to object that it might be drizzling rather than raining (drizzle being defined as droplets smaller than raindrops), then we would need either a precising or a theoretical definition to specify the difference. Once agreement on definition is achieved, the facts can be ascertained tomorrow: today, we can only know the truth value is yet to be determined, much in the same way we might not know the answer to a math problem until we completed the calculation.

      If you disagree with this analysis and/or you are interested in the problem of “future truths” you might be convinced that Aristotle's four-and-a-half page solution to the problem of future truths in his “The Sea-Fight Tomorrow” is a better solution than that stated here.

   3. Open the door, please.

      Answer
      

      The request can be obeyed or not, but this use of directive language is not said to be true or false. Thus, this sentence is not a statement.

      That being said, several different theories of a logic of imperatives has been proposed based on satisfiability or avoidance of contradiction in obligation or conduct instead of truth values.

   4. The blue whale (Balaenoptera musculus) is the largest fish ever to exist.

      Answer
      

      Since whales are mammals, not fish, the truth value is false, so the sentence is a statement as it has the truth value of false.

   5. “Yond Cassius has a lean and hungry look; He thinks too much: such men are dangerous.” — quotation from Shakespeare's play Julius Cæsar[8]

      Answer
      

      As taken from a work of fiction, strictly speaking, these sentences do not have a truth value. Ordinarily, fictional sentences are not taken to be statements. In the case of this play, the fictional work is based on an imagined dramatic creation of a historical event. Nevertheless, we can speak of truth in accordance with the consistency of sentences in a work of fiction. So, in this sense, works of fiction can be in part evaluated in terms of their “fictional truth” — ie, whether the sentence, if true, is consistent with other sentences in the work.

   6. Pegasus, a creature often mentioned in Greek mythology, has wings.

      Answer
      

      This sentence is sometimes taken to be a statement true by definition. However, classical theorists argue that the subject of a sentence must exist in some sense in order for the sentence to be meaningful. In classical (Aristotelian) logic, existence of the subject is usually assumed to exist; if the subject does not exist, then the sentence is normally not regarded as a statement. Nevertheless, modern logic does not assume the “existential import” (the existence of the subject of the statement) and regards general statements as meaningful in a conditional sense: e.g., “Pegasus is a winged horse,” is taken to mean “If something is Pegasus” then it is a winged horse; this view is maintained independently of whether or not Pegasus actually exists.

   7. “When we hate a person, what we hate in his image is something inside ourselves.”[9]

      Answer
      

      This sentence is either true or false and so is a statement.

   8. “Let the people who never find true love keep saying that there's no such thing.”[10]

      Answer
      

      In most contexts, this sentence would not be a statement, as imperative sentences are usually neither true nor false. Imperatives typically begin with verbs and usually give request or advice. However, in a specific context where someone has denied that there is not such thing a true love, the sentence might be taken to mean there is such an experience. In this case the imperative should be regarded as a statement.

   

   9. ”You shall create beauty not to excite the senses but to give sustenance to the soul.”[11]

      Answer
      
      

      The sentence is not one with a truth value since it is typically an imperative sentence which expresses a instruction — which can be either accomplished or not accomplished. The content of the imperative is either possible or impossible but not true or false, so this sentence is not a statement in an everyday context.

   10. “The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas.”[12]

       Answer
       

       Although there is a reference to an “ideal” entity in this sentence, this is an accurate description of a formula that approximates the behavior of many different gasses bases on the pressure, volume, and temperature of a gas. Since the description is in accordance with the way the law is used the sentence is usually regarded as a true statement.

       
       
       

6. Optional: Further Differences Between a Statement and a Sentence.

   1. Consider whether there are two statements in the box below:

      A Republican is President (of the U.S.).

      A Republican is President (of the U.S.).

      
      

      1. Aside from the uncertainty of when the statements are uttered, of which president is meant, and so on, we would probably reply there are only one statement but two sentences in the box. To explain this reply, sometimes logicians make a distinction between a sentence token (the ink, chalk marks, or pixels present of which there are two in this example) and a sentence type (the meaning of the marks present of which there is just one meaning). On this account, a sentence type is not considered to be a statement unless it is used to refer to a specific person at a specific place and time.

      2. Every distinct statement, apart from universal statements, is a particular historical event as it implicitly occurs at specific time, place, and circumstance.

         
         

   2. Some further differences between a sentence and a statement noted by logicians include:

      1. The same statement can be expressed by two different sentences. E.g., the sentence …

         ”The cup is half-empty.“

         expresses the same statement as …

         “The cup is half-full.”

         … even though the two sentences differ in emotive significance.

      2. A sentence can express different statements at different times. E.g., the same sentence …

         “The current president of the Philippines is Marcos.”

         … as expressed in 1980 and 2025 expresses two different statements since Ferdinand Marcos was president in 1980 and Bongbong Marcos was president in 2025. Both the name “Marcos” and the phrase “current president” are termed “indexicals” since the meaning of these expressions is dependent on the context in which it is used.

      3. A statement is independent of the language in which it is asserted, but a sentence is specific to the language in which it is expressed. E.g., the sentences …

         “Das ist immer noch viel.”

         “But that is still a lot.”

         “C’est encore beaucoup.”

         express the same statement ceteris paribus.[13]

      4. A sentence can express an argument composed of several statements. E.g., from a study of instability in Nigeria, this sentence …

         ”Ethnic determination is often based on 19th century European designations of convenience because true Nigerian cultural associations are multi-faceted and often indistinct.”[14]

         … can be interpreted as two or three different statements — depending on how we choose to analyze it. Normally, the sentence would be considered as being composed of two premises and a conclusion. Thus, this sentence would be composed of three statements which were made to express an argument:

         Nigerian cultural associations are multi-faceted.

         Nigerian cultural associations are indistinct.

         ∴ Nigerian ethnic determination is often based on 19th century European designations.

         The conclusion does not logically follow from the premises as they stand. An additional implicit background premise needs to be added stating that aside from the existing Nigerian cultural associations which are difficult to distinguish, the only remaining convenient determination is based on the (less than ideal) 19th century European designations.

         
         

7. Frequency of use of words “argument,” “statement,” “proposition,” and “sentence” use in Google books 1800-2022. Ngram Viewer

   
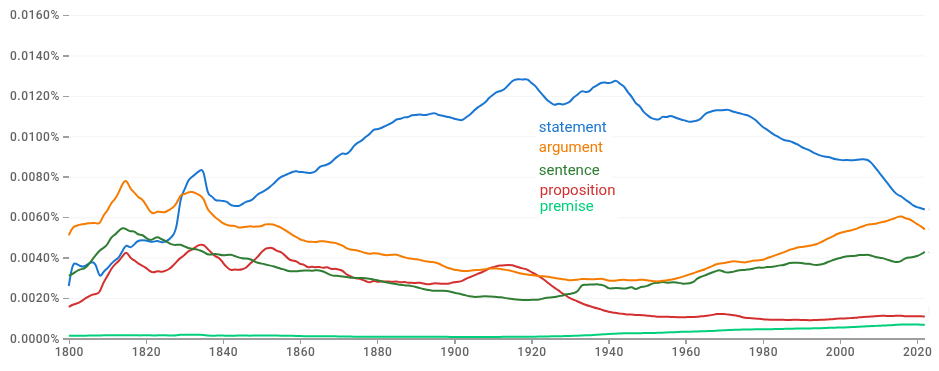
   FIG. 1. Historical Frequency of Use of “argument,” “statement,” “proposition,” and “sentence” in Google Books 1700-2010.
   
   
   

8. A Distinction Between a Statement and a Sentence

   postscript

   “To make a statement is to utter an indicative sentence for the purpose of asserting something … [P]ersons who utter the same indicative sentence do not necessarily make the same statement, and one person may make different statements by uttering the same indicative sentence on different occasions, e.g. by saying on different days ‘Today I am sitting in front of a stove.’. On the other hand, a man may utter two different indicative sentences at different times and thereby make the same statement twice, e.g. by saying on successive days ‘I am sitting by a stove today’ and ‘I was sitting by a stove yesterday.’ ”
   
   William Calvert Kneale and Martha Kneale, The Development of Logic (1962 Oxford: Clarendon Press, 1984), 50.
   
   

9. Links to Additional Examples

   Test your understanding of the distinction between statements and nonstatements in the following quiz:

   Quiz: Statements and Nonstatements

Notes